Примеры современных охлаждаемых турбин

	Типичный вид турбины высокого давления с сопловой и рабочей лопатками

4 ПОРЯДОК РАСЧЕТА ТЕПЛОВОГО СОСТОЯНИЯ
ОХЛАЖДАЕМЫХ ТУРБИННЫХ ЛОПАТОК

Снижение температуры охлаждаемых лопаток относительно температуры газа обуславливается теплообменом между лопаткой и газом, теплообменом между лопаткой и охлаждающим воздухом, а также распространением тепла в самой лопатке. Различные условия подвода тепла и отвода его в охлаждающий воздух через поверхность приводят к значительной неравномерности поля температур в теле лопатки. Для определения поля температур необходимо решать пространственную задачу теплообмена в многосвязной области с граничными условиями, переменными в пространстве и времени.

В общем случае, температура в любой точке лопатки является функцией трех координат и времени: .

Распространение тепла внутри лопатки описывается уравнением Фурье-Кирхгофа

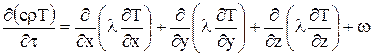(4.1)

где с - удельная теплоемкость;

r - плотность;

l - коэффициент теплопроводности;

w - интенсивность внутренних источников тепла.

(4.1) – нелинейное дифференциальное уравнение в частных производных. Его решением является температура как функция координат и времени.

Аналитическое решение этого уравнения имеется только для тел простой формы. Поэтому для лопатки оно решается численными методами – например, методом конечных элементов. Для предварительных расчетов целесообразно принять предложение, что . Тогда задача становится двумерной и сводится к рассмотрению поперечного сечения лопатки.

На установившемся режиме работы двигателя . Учитывая отсутствие внутренних источников тепла, можно упростить уравнение (4.1):

, (4.2)

где – коэффициент температуропроводности (в общем случае зависящий от температуры).

Для решения уравнения (4.1) необходимо задать начальные и граничные условия, а для решения уравнения (4.2) – граничные условия.

Начальные условия задают распределение температуры в некоторый начальный момент времени:

(4.3)

Различают четыре вида граничных условий.

Граничные условия первого рода задают распределение температуры на всей поверхности лопатки, в общем случае переменное во времени:

, (4.4)

где «пов» координаты поверхности (внутренней и наружой).

Граничные условия второго рода задают распределение плотности теплового потока

. (4.5)

Граничные условия третьего рода задают распределение температуры наружного потока и коэффициента теплопроводности:

;

;

; (4.6)

,

где 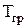- температура газа на наружной поверхности лопатки (греющая температура);

- температура воздуха на внутренней поверхности (охлаждающая температура);

и - коэффициенты теплоотдачи на наружной и внутренней поверхностях.

Граничные условия четвертого рода используются при контактном теплообмене (например, лопатки с диском через замок).

Задается температура контактирующей детали и коэффициент теплообмена.

При определении температурного поля в охлаждаемых лопатках используют граничные условия 3-го рода.

Форма и размеры лопатки, в том числе наружного профиля и внутренних каналов, задаются выбранной конструктивной схемой, которая определяет и направление течения охладителя.

Параметры газа, обтекающего решетки профилей, и охлаждающего воздуха, определяются из газодинамического расчета двигателя и турбины. Определение коэффициентов теплоотдачи от газа к лопатке и от лопатки к охлаждающему ее воздуху является одной из центральных задач, решаемых в процессе теоретических и экспериментальных исследований.

Дата добавления: 2015-08-26