Темперированный строй

В современных музыкальных инструментах с фиксированным строем используется только одно натуральное отношение – октава. Частоты или длины волн звуков, составляющих октаву, относятся как целые числа 1:2. Это можно продемонстрировать, если взять струну опреде­ленной длины и разделить ее пополам. Звук, издаваемый половиной струны, будет на октаву выше звука целой струны. Все прочие музы­кальные отношения – квинты, терции, тона, полутона наших роя­лей и органов не являются отношениями целых натуральных чисел. Каждая из восьми октав, обнимающих в своей совокупности диапа­зон частот, используемых в музыке, разделена на двенадцать лога­рифмически равных интервалов – полутонов. Это означает, что логарифмы длин во всем прочем одинаковых струн, издающих тона, соответствующие любым двум соседним ступеням внутри октавы, отличаются друг от друга на постоянную величину. Если взять стру­ну длиной L, точки, соответствующие n-ой ступени вниз от основного тона, можно найти по формуле 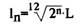(1):

(1)

тогда

log1_n - logl_n-1 = ¹/₁₂ log2 = const

при n=0 1 ₀ =L

при n=12 1 ₁₂ =2L

То есть двенадцатая ступень соответствует струне удвоенной дли­ны, октаве вниз от основного тона. Все промежуточные ступени вы­ражаются иррациональными, а не натуральными числами. Такой темперированный строй является сейчас общепринятым. Он счита­ется удобным для исполнения произведений, созданных исходя из совершенно других принципов, а именно – из принципов натураль­ного лада, где отношения ступеней выражаются натуральными чис­лами. Другие способы темперации оказались по разным причинам неприемлемыми.

Однако существует скептический взгляд, обращенный к двум ос­новным моментам, – к музыкальной практике, использующей этот строй, и к культуре самого строя. Несмотря на формальное равнопра­вие двенадцати ступеней, в практике композиции некоторые тона играют более важную роль, чем другие, это выражается, в частности, в разделении клавиш одной октавы на группы белых и черных. Уви­дев в этом нелогичное ограничение свободы композитора традициями лада, Шенберг предложил уравнять в правах все двенадцать тонов октавы и подал тому пример собственным творчеством. Однако, ос­тавалось неясным, почему же сохраняется натуральное, "ладовое" по природе, отношение октавы 1:2 и почему каждая из восьми октав разделяется на двенадцать, а не на какое-нибудь иное количество ступеней. Ведь формулу (1) можно записать в более общем виде:

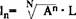
где А – любое действительное число

N – целое число

Современному интеллекту выбор N = 12 представляется осно­ванным на столь же неоправданно мистических или косно тра­диционных соображениях, как и разделение года на 12 месяцев, небесной сферы на 12 секторов, соответствующих 12-ти знакам Зодиака, счета дюжинами и т.п. Однако разумные основания для выбора каких-либо иных значений А и N, по-видимому, отсут­ствуют, и критика успокоилась на том, чтобы принять сущест­вующие значения А=2 и N==12 как основанную на привычном удобстве конвенцию. С другой стороны, додекафония Шенберга, хотя и получившая известное развитие в XX веке, не заменила традиционной музыки. Причина этому – на наш взгляд – в нарушении додекафонистами некоторых онтологических прин­ципов музыкального строя, не компенсируемых ни формальной логикой теоретиков, ни мастерством и талантом композиторов. Ибо логика додекафонистов основывалась на предположении о самоочевидной необходимости темперированного строя и не принимала во внимание того обстоятельства, что самая темпе­рация была лишь вынужденным компромиссом между онтологи­ческой структурой музыкального строя и техническими средст­вами исполнения музыки.

Автор видит свою задачу в том, чтобы объяснить необходи­мость выбора числа N=12 для ступеней октавы, тем самым обна­ружив следы онтологических принципов в темперированном строе, и предложить двенадцатитоновый натуральный строй.

Дата добавления: 2015-08-26