Задание 3. Транспортная задача

В m заводах имеется однородный груз продукции в количествах 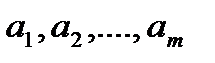. Этот груз нужно перевести n потребителям, потребности которых равны . Стоимость перевозки единицы груза из i – го завода j – ому потребителю равна (таблица 3). Требуется составить план перевозки груза с заводов потребителям, при котором суммарные расходы на перевозку будут минимальными.

Таблица 3

Заводы	Потребители	Запас продукции, ед.
В1	В2	В3	В4
А1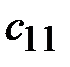
А2
А3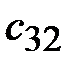
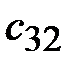
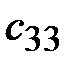
Потребность в продукции, ед.

Исходные данные по вариантам заданий указаны в таблице 4.

Таблица 4

Вар

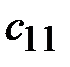
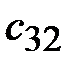
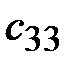
План решения задачи:

1. Выбрать из таблиц исходные данные своего варианта.

2. Вычертить матрицу транспортной задачи, проверить ее на закрытость. Если задача открытая, то привести ее к закрытой, добавив в матрицу задачи фиктивного поставщика, или покупателя.

3. Записать в матрицу транспортной задачи первый опорный план, пользуясь одним из известных вам способов построения опорного плана (способ северо-западного угла, наименьшей стоимости, двойного предпочтения).

4. Проверить построенный опорный план на вырождение. Если надо, принять меры для преодоления вырождения опорного плана.

5. Рассчитать значение целевой функции для опорного плана.

6. По правилам метода потенциалов рассчитать потенциалы строк и столбцов.

7. Используя найденные потенциалы, проверить построенный опорный план на оптимальность.

8. Если решение оптимальное перейти к пункту 12.

9. Если решение неоптимальное, его нужно улучшить. Для этого надо найти клетку матрицы транспортной задачи, подлежащую улучшению, построить для неё замкнутый цикл, определить объём ресурсов для перемещения по вершинам этого цикла.

10. Выполнить перемещение ресурсов по вершинам цикла, не нарушая баланса по строкам и столбцам матрицы.

11. Перейти к пункту 5-7.

12. Выписать оптимальное решение и провести его экономический анализ.

Дата добавления: 2015-08-20