Профилирование относительно высоких (длинных) лопаток

Существующие способы профилирования относительно высоких (длинных) лопаток основаны на использовании радиального равновесия потока в осевых зазорах. Рассмотрим ступень с цилиндрическими обводами (рис.17.1.).

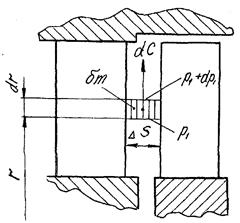
Рис. 17.1. К выводу уравнения радиального равновесия

Выделим в осевом зазоре двумя цилиндрическими сечениями на радиусе r элементарное кольцо толщиной dr и шириной 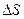. Выделенное кольцо с массой 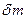вращается в осевом зазоре с окружной скоростью С_1u и на него действует центробежная сила dC.

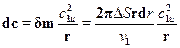
где v ₁ - удельный объем в зазоре на радиусе г.

Указанная центробежная сила уравновешивается силой dP₁, обусловленной разностью давлений dP₁ на наружной и внутренней поверхности выделенной частицы потока

.

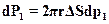Приравнивая силы dС и dP₁ находим условие радиального равновесия потока в осевом зазоре

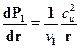. (17.1)

При отсутствии потерь в сопловой решетке из уравнения количества движения имеем

.

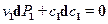Выражая из последнего уравнения dP₁ и подставляя его в (17.1), получим

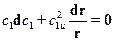. (17.2)

Учитывая, что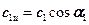

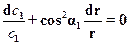. (17.3)

Уравнение (17.2) и (17.3) являются исходными при выборе методов профилирования относительно высоких лопаток.

Наиболее распространенным способом профилирования лопаток газовых турбин является закрутка лопаток по методу постоянной циркуляции. При этом обеспечивается безударный вход потока на рабочие лопатки и сохраняются постоянные по высоте лопаток осевые составляющие скоростей С_1a за сопловой и С_2а за рабочей решетками, что уменьшает неравномерность поля скоростей в ступени.

Дифференцируя уравнение 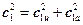, получим 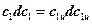. После подстановки в выражение (17.2) имеем

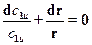. (17.4)

Проинтегрировав уравнение (17.4), получим условие постоянства поля осевых скоростей за сопловой решеткой при изоэнтропийном течении:

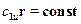. (17.5)

Аналогично условие постоянства поля осевых скоростей за рабочей решеткой: C_2ur = const.

Записывая полученные условия для корневого и произвольного сечений, а также учитывая соотношения треугольников скоростей получим зависимости для изменения углов α₁, β₁, β₂ в сопловой и рабочей решетках по радиусу ступени при закрутке лопаток по методу постоянной циркуляции:

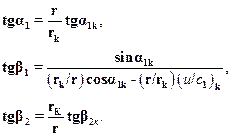
Полагая, что параметры рабочего тела перед ступенью и за ней не меняются, изменение степени реактивности в ступени по радиусу при условии постоянства коэффициента скорости φ определяется следующим образом

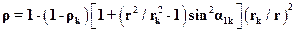(17.6)

Особенностью ступени, спрофилированной по методу С_1a=const является постоянство работы во всех сечениях по высоте лопатки.

Наиболее распространенным способом закрутки лопаток паровых турбин является закрутка их при сохранении неизменным угла выхода потока из сопловой решетки (α₁=const). Достоинство рассматриваемого метода заключается в том, что сопловые лопатки ступени остаются цилиндрическими, что упрощает технологию их изготовления. Для определения закона изменения угла β₂ по радиусу необходимо дополнительное условие. Чаще всего оно записывается в виде: Lu=const или β₂=const по радиусу ступени.

Дата добавления: 2015-08-20