Уравнения радиального равновесия в ступени

Паротурбинные ступени с q=d/l<10 относят к ступеням с длинными лопатками (ступени большой веерности), в которых изменяются термодинамические параметры и кинематические характеристики потока рабочей среды вдоль радиуса ступени (по высоте решеток). Эти изменения следует учитывать при профилировании проточной части сопловых и рабочих решеток, чтобы обеспечить высокий КПД ступени. На рис.9.1,а показана проточная часть ступени большой веерности с меридиональными линиями тока и расчетными сечениями, а на рис.9.1,б – параллелепипед абсолютных скоростей в цилиндрической системе координат. Для этих условий вектор скорости раскладывается на три составляющие: с²=с_u²+c_a²+c_r², которые связаны между собой через соответствующие углы: a, n,. Чтобы спрофилировать лопатки для такой ступени, необходимо знать зависимости изменения параметров вдоль радиуса в зазорах между решетками. Для этого получим уравнение, связывающее изменение давления р₁ вдоль радиуса со скоростью с₁. Рассмотрим ступень, в которой линии тока расположены на цилиндрических поверхностях, т.е. составляющая с_r=0. Будем считать, что поток в ступени осесимметричный, т.е. параметры потока в окружном направлении неизменны. Тогда для вывода уравнения радиального равновесия элементарной частицы среды рассматривается схема, показанная на рис.9.1,в. Элемент потока толщиной da выделен в зазоре между цилиндрическими сечениями радиусами r и r+dr и меридиональными плоскостями с углом dj от оси ротора. К выделенному элементу приложены силы давления: по цилиндрическим поверхностям +р₁rdjda и –(р₁+dр₁)(r+dr)djda; по меридиональным поверхностям р₁drda, а также инерционная сила от центростремительного ускорения элемента , где с_1u – окружная составляющая с₁.

Рис.9.1. К характеристике линий тока (а), скоростей (б) в ступени большой веерности и к выводу уравнения радиального равновесия потока в ней (в)

Поскольку давление р₁ вдоль оси а постоянно, то уравнение равновесия всех сил в проекциях на направление радиуса r имеет вид:

р₁rdjda-–(р₁+dр₁)(r+dr)djda+2р₁drdasin 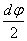+ =0. (9.1)

Заменив sin(dj/2)»dj/2, после простых преобразований получим упрощенное уравнение радиального равновесия для сечения 1-1 ступени

. (9.2)

Аналогично получают уравнения и для других сечений (0-0 и 2-2): ; .

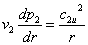Применительно к схеме течения рис.9.1,б, где присутствуют и составляющие скорости по радиусу с_1r и вдоль оси а – с_1а, уравнение (9.2) записывается следующим образом:

. (9.3)

В правой части (9.3) первый член характеризует влияние центробежных сил, а остальные члены – влияние радиального ускорения. Итак, для подбора решеток важно знать изменение скоростей

52.Профилирование относительно высоких (длинных) лопаток.

Дата добавления: 2015-08-20