РЕФЕРАТ 2 страница

1.2.3 Құрамында фторы бар полимерлердің гидрофобты материал ретінде қолданылуы

1938 жылы АҚШ Дупонт химиялық компаниясы фтор қоспасындағы полимерін жетпіс жыл зерттеген, ертеректе зерттелген фтор қоспасындағы полимерлердің ішінде PTFE, PVDF сияқты бірінші дәрежелі фтор қоспалы жоғары молекулалы қосылыстарды бақылаған. Бұл заттардың құрылысы жағынан басқа полимерлерден ерекше, яғни, балқуға төзімді, химиялық тұрақты, жоғары температураға төзімді, бірақ өндіру біршама қиын, заттарды қаптау кезінде жоғары температураны қажет етеді. Екінші дәрежелі фтор құрамды полимерге фторолефин жатады, полимер құрамына фторсыз сомономер енгізілсе кристаллдану температурасы төмендейді. Жоғарыдағы PTFE, PVDF полимерлері кристаллды полимерлерге жатады, ерітілген күйде сыр ретінде қолданылады. Құрғақ жерде 230 температурада кристаллданады. Тефлон әдетте температураға төзімділігі үшін металл беттерін қаптап, коррозияға төзімді материалдар ретінде және ас пісіру қазанының ішкі қабырғасына отырғызып, лиофобты материал ретінде де қолданылады.

Құрылыс жұмыстары үшін 1982 жылы Жапонияда lumiflon деп аталатын фторолефин және винил эфирінің сополимерін қолданып фторлы мономерді ароматты көмірсутек және кетон еріткіштерінде ерітіп, фторлы полимерді жасап шығарды. Оны темпетатураға төзімді материал ретінде ластанбайтын қасиетіне қарап қолданды.

1.2.4 Фторлы полимерлердің ұшақтың мұздануға қарсы материалы ретінде қолданылуы және дамуы

FEVE түріндегі мономер, фторлы акрилат шайыры және тізбектелген цианаттар мен изоцианаттардың ортақ ерігіштілігі бар, әдетте қыздыру барысында кристаллданады. Құрылыс материалы ретінде қолдануға тиімді. Ұлыбритания Desoto компаниясы ХХ ғасырдың 90 жылдарынан бастап фторлы шайырды ұшақтың сыртқы бояғышы ретінде қолданған, 20 жылдан кейін қазіргі полиуретанды сырлар бір есеге артты. Жапония авиациялық сырды зерттей келе, полиуретанды жүйелердің 150 температураға дейін шыдамдылығын ашты. Жапония жоғары дәрежелі сыр өндіру компаниясы және Жапония Fuji Heavy компаниясы бірлесіп, жаңа зат ойлап тапты. Силикатты шайырды полиуретанға қосып, жоғары температуралы радиоактивті сыр өндірді. Жапония Asahi Glas компаниясы LUMIFLON түріндегі бояғыш сырды жасады (12-сурет).

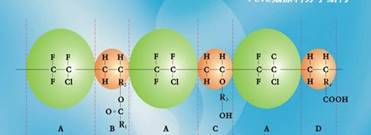
Cурет 12. LUMIFLON түріндегі гидрофобты бояғыш сыр

Негізінен фтор қоспалы полимерлер ертеректен бастап авиация жұмыстарына қолданылған. Ұшақта гидрофобты материалдар қолданылса, ұшақтың мұздануға қарсы жүйеге көмегін тигізіп қана қоймай, комплексті коррозияға қарсы қасиет көрсетеді. Мұздануға қарсы жүйеге супергидрофобты материалдардың әсерін зерттеуді АҚШ профессоры Amirfazli ұсынған. Оның идеясы ұшақтың мұздануға қарсы жүйесіндегі энергия шығымына гидрофобты материалдардың әсерін зерттеу.

Бұл зерттеу жұмыстары қазірге дейін аэродинамикалық трубада ұшақтың ұшу моделін қолданып, дүние жүзінде 10-ға жуық рет тәжірибеден өткізілген, жұмыстың мақсаты, әдеттегі қанат беті мен супергидрофобты қанат бетінің мұздану жағдайын салыстыру.

2.ТӘЖІРИБЕЛІК БӨЛІМ

2.1 Судың физикалық қасиеті

Ұшақтағы мұздану процессі судың қасиеттеріне тығыз байланысты болады. Таза су —түссіз, иіссіз, дәмсіз сұйықтық. Қалыпты қысымда 100°С-та қайнайды да, 0°С-да мұзға (р=0,92 г/см³) айналады. Жылу сиымдылық жағынан ең жоғары сұйықтық болып есептеледі. Оның құрамы сутек және оттек атомдарынан тұрады, бір оттек атомына екі сутек атомы шамамен 105⁰ арқылы қосылған (13-сурет), сондықтан су өте бейтарап зат [10].

Cурет 13. Cудың геометриялық құрылымы

Судың электрондық құрлымы: оттек:

сутек:

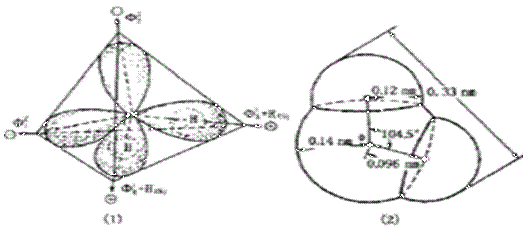
Сурет 14. Cудың геометриялық кеңістіктегі формасы

Судың агрегадттық күйі, қайнау температурасы, қату температурасы қысымға байланысты әртүрлі болады. Ал тығыздығы температураға байланысты өзгеріп отырады (15-сурет).

Сурет 15. Cудың тығыздығының температураға тәуелділігі

Судың агрегаттылығы температураға байланысты өзгереді, судың жылу сиымдылығы өте жоғары болғандықтан сұйық күйден қатты мұз күйге ауысу барысында молекуланың реттілігі және бір біріне тартылу бағыты да өзгереді. Әдетте сұйық күйдегі су молекуласының бір бірімен тартылуы сутектік байланыс арқылы жүзеге асады, олардың арасы тетраэдр формалы болады (16-сурет), ол байланыстар үздіксіз қозғалыста болады, бұл байланыстар температураның жоғарылауына байланысты төмендейді (1-кесте) [11].

Температура （℃）	Координациялық сан	Молекулалар арасы (nm)
		0.276
1.5	4.4	0.290
8.3	4.9	0.305

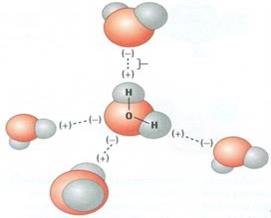
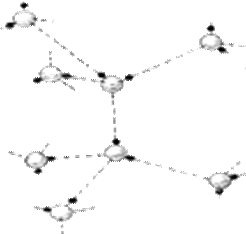
Сурет 16. Cұйық күйдегі су молекуласының өзара байланысу құрылымы

Сұйық күйдегі су молекуласы немесе су булары сутектік байланыспен байланысқан, су молекулалары арасындағы байланыс біршама әлсіз, сондықтан еркін қозғалғыштығы жоғары болады. Ал мұздану барысында судың қозғалғыштығы әлсірейді, ал сутектік байланыс біршама жоғарылап, кристалл пайда болып, тұрақты алты қырлы молекулалар шоғыры түзіледі (17-сурет). Ал молекула шоғырлары өзара бір біріне тартылу барысында шоғырлар арасында бостық пайда болады, сол себептен мұздану барысында судың көлемі артады.

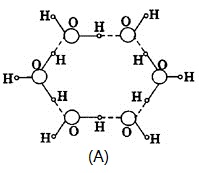
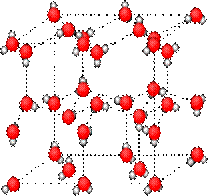
Сурет 17. Cу молекулаларының бір біріне тартылып шоғыр түзілуі (A) және шоғырлардың өзара тартылып бостық жүйе түзілуі (B).

Түзілген бостық жүйелер арасында және тартылыс когезиясы пайда болады, кристаллдар бір біріне жақындап кристаллдың көлемін ұлғайтады, бұл процесс белгілі ретпен жүреді (18-сурет). Кристаллдар бір біріне үздіксіз тартыла береді, бұл процесстің себебі сутектік байланыстың шамасына байланысты. Кристаллдану уақытына байланысты кристаллдардың формасы да әр түрлі болады, бірақ кристаллдар негізінен алты қырлы болады [12].

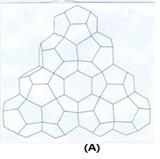
Cурет 18. Бостық жүйелердің бір біріне тартылып кристалл формасын түзуі (A) және кристаллдану уақытына байланысты кристаллдардың формасының әртүрлі болып жиналуы (B) және кристалдардың когезиясы (C).

Түзілген толық кристаллдардың тұтқырлығы өте жоғары әрі суға қарағанда қатты денемен адгезиялануы да жоғары болады. Әсіресе тұманның адгезиясы өте жоғары. Себебі, тұман үш фазадан тұрады, дымқылдық құрамы мұзға қарағанда жоғары әрі құрлымы да мұздан күрделі. Құрамында судың үш түрлі агрегаты сақталған (19-сурет). Тұман төмен температуралы ауа райында пайда болады, ол ауа ағысы әсерінен жабысқақ күйге айналып, суық қатты денеге тигенде толық кристаллға айналып, әрі көлемін үлкейтіп адгезиясын бірте бірте арттырады. Ал сұйық күйдегі су ауа ағысы әсерінен алдымен қатты денеге адгезияланады, содан соң төмен температура әсерінен кристаллданады.

Сурет 19. Тұманның құрамы. Қатты (A), сұйық (B), газ (C) күйдегі су

Кристаллдану барысында егер жанасқан қатты бетке әр түрлі тереңдікте жанасқан болса, көлем өзгерту барысында адгезия жұмысы артады, мұз қату жоғары болады.

Мұздың құрлысыкристаллдардың қабат бойынша орналасуына байланысты өседі, алты қырлы кристаллдардың арасында когезия күші болғандықтан бір бірімен қосылып, күрделі кристалл торын түзеді (20-сурет). Бірақ әр қабат арасындағы тартылыс күш әр қабаттағы кристаллды құрайтын жүйе арасындағы тартылыс күшке қарағанда өте әлсіз болады.

Cурет 20. Мұздың кристалл қабатының өсуі. Төбесінен қарағанда (a) және жанынан қарағанда (b).

Мұз түзілу кинетикасын Masakazu Matsumoto 230K температурада зерттеген. Мұздың кристаллдануы негзінен төрт бөлімнен тұрады [13,14].

1) Тыныштықтағы химиялық потенциалдың тұрақты уақыты

（t＝256–290 ns）;

2) Қысқа уақытты химиялық потенциалдың уақыты （t＝290－320ns）;

3) Қысқа уақытты химиялық потенциалдың үдеу уақыты

（t＝320－360ns）;

4) Тоқтау уақыты, химиялық потенциялдың тұрақтануы кезінде мұз толық түзіледі （t＞360ns）.

2.2 Гидродинамика және оның аэродинамикамен байланысы

Ұшақтың ұшуы негізінен ауа тұтқырлығымен өте тығыз байланысты болатындықтан аэродинамикалық параметрлер гидродинамиканың заңына бағынады. Гидродинамика көмегімен сұйықтықтың жалпы қасиеттеріне механиканың негізгі заңдары мен тәсілдерін қолдана отырып, сұйықтық алып жатқан тұтас ортаның кез келген нүктесінің жылдамдығы, қысымы тәрізді өлшемдер анықталады. Гидродинамика көмегімен сұйықтықтың жалпы қасиеттеріне механиканың негізгі заңдары мен тәсілдерін қолдана отырып, сұйықтық алып жатқан тұтас ортаның кез келген нүктесінің жылдамдығы, қысымы тәрізді өлшемдер анықталады [15].

Гидродинамиканың негізгі тәсілдері дыбыс жылдамдығынан (шамамен 330 м/сx1200 км/сағ) жылдамдығы төмен газ қасиеттерін зерттеу үшін де пайдаланылады. Гидродинамика теориялық гидродинамика және эксперименттік гидродинамика болып екіге бөлінеді. Теориялық гидродинамикада сұйықтықтың жеке бөлшектері сұйық орналасқан тұтас ортаның материалдық нүктелері ретінде қарастырылады немесе сұйықтық алып жатқан кеңістіктегі жылдамдықтар өрісі зерттеледі. Гидродинамика тұрғысынан алғанда сұйықтықтың ең басты қасиеті – аққыштық пен тұтастық. Сұйықтықтың газ тәріздес ортадан негізгі айырмашылығы – оның сығылмайтындығы. Мұндай сұйықтықтар үшін үзіліссіздік теңдеуі мен Навье-Стокс теңдеуі қолданылады. Тұтқыр сұйықтық қозғалысы қарастырылғанда, ағыс сипаттамасы болып табылатын өлшемсіз шама – Рейнольдс саны қолданылады. Эксперименттік гидродинамика тәсілдерінің қатарына сұйықтық қозғалысы мен оған шекаралас орналасқан қатты дене маңындағы ағысты кішірейтілген масштабта қайта жасап алуға негізделген модельдеу тәсілдері жатады. Гидродинамиканың көптеген есептерін шешуге ұқсастық теориясы мен ұқсастық өлшеміне негізделген гидродинамикалық тәжірибелер де қолданылады. Гидродинамика әдістері гидравлика, гидрология және гидротех. есептерін шығаруды, гидротурбинаны, сорғыларды, құбырларды, т.б. есептеуді табысты шешуге мүмкіндік береді [16,17,18]. Гидродинамиканың аэродинамикаға байланысты параметрлері қысымға, температураға, жылдамдыққа тәуелді болады. Негізгі теңдеулері:

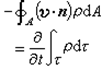
Қозғалатын жүйеде, мысал ұшақтың ұшуы кезінде негізгі теңдеулер интегралды форма және дифференциалды форма болып екіге бөлінеді. Интегралды форма басқару жүйесі және басқару беті арасындағы интеграл арқылы аққыш дене мен физикалық күш арасындағы интегралды байланысты көрсетеді. Ал дифференциалды форма шексіз кіші басқару жүйесі немесе жүйенің тікелей формасында кез келген нүктедегі аққыш дене мен физикалық күштер арасындағы дифференциалды байланысты көрсетеді. Интегралды форманың формулалары арқылы тұтас дененің қасиеттерінің байланыстарын шешуге болады, мысалы аққыш дене мен физикалық күш арасындағы қорытқы күшімен жалпы энергиялардың алмасуы. Дифференциалды форманы шешуде немесе шексіз кіші басқару жүйесінен туындаған интегралды форманы шешуде қолданылатын негізгі формуламен аққыш дененің детальін және аққыш дененің әр нүктесіндегі физикалық күшті табуға болады.

Интегралды форманың негізгі формулалары: үздіксіз формула, импульстік формула, мезеттік импульс формуласы және энергиялық формула болады.

1) Үздіксіз формула, ол бірлік уақыт ішінде аққыш дененің басқару органының сапасы ішкі массасының артуына тең болады. Ол массалар сақталу заңына байланысты шыққан. Математикалық формуласы：

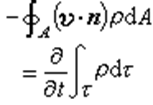
Мұндағы, v-жылдамдық; ρ- тығыздық；τ- басқару органының көлемі；A- басқару органының ауданы; n- dA басқару бетіндегі сызықтық бағыттау саны (21-сурет). Әдетте ағыс барысында теңдеудің оң жағы нольге тең болады. Бұл кезде түтікше параметрі (22-сурет) төмендегідей болады:

ρ₁v₁A₁=ρ₂v₂A₂

бұл жерде ρ_1, v₁, ρ₂, v₂ парамертлері A ₁ және A₂ беттегі аққыш дененің тығыздығы мен жылдамдығы.

Сурет 21. Интегралды теңдеудің негізгі параметрлері

Сурет 22. Түтік ішіндегі аққыш дененің қозғалыс параметрі

2)Импульс теңдеуі. Бірлік уақыт ішінде басқару органына енген импульс және басқару бетіндегі сыртқы күштің қосындысы басқару органы ішіндегі энергияның артуына тең болады. Ол импульстің сақталу заңына бағынады. Математикалық жолмен төмендегідей болады.

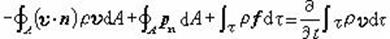
Мұндағы, - dA басқару бетіне түсірілген сыртқы күш, f-dτ басқару бетіне түсірілген сыртқы күш, көбінесе ауырлық күші қарастырылады. Әдетте теңдеудің оң жағы нольге тең болады. Импульстік теңдеу көбінесе аққыш дене мен сыртқы ортаның әсерлесу күшін есептейді.

3) Мезеттік импульс теңдеуі. Бірлік уақыт ішінде аққыш дененің басқарушы денеге ағып кіру импульсі және басқарушы дене мен басқарушы беттегі сыртқы күштің белгілі санақ нүктесіндегі импульс мезеттігінің қосындысы, бұл басқарушы денедегі ұқсас бір нүктедегі импульс мезеттігінің артуына тең болады. Ол импульс мезеттілігінің сақталу заңынан шыққан. Математикалық формуласы төмендегідей:

Мұндағы, r- белгілі санақ нүктесінің “0”бастапқы нүктеден dA басқару бетіне немесе dτ басқару бетіне барудағы векторы. Әдетте теңдеудің оң жағы нольге тең болады. Ол трубомашиналы теңдеуден шыққан.

4) Энергия теңдеуі. Белгілі бірлік уақыт ішіндегі басқарушы денеге ағып кірген әртүрлі энергия және сыртқы күштердің жұмысының қосындысы, Бұл басқарушы дене ішкі энергиясының артуына тең. Ол энергиялар сақталу заңына бағынады. Математикалық формуласы төмендегідей.

Мұндағы, q_λ -бірлік уақыт ішіндегі бірлік аудандағы, dA басқарушы бетіндегі тасымалданған энергия. q_R -бірлік уақыт ішіндегі бірлік массаның dτ басқарушы бетте алынған тасымалданбаған энергия. Ол сәулелену энергиясын, химиялық реакциядан шыққан энергияны қамтиды. E-бірлік массадағы аққыш дененің ішкі толық энергиясы. Ол энергиялар ғылымындағы ішкі энергия, электромагниттік энергия сияқтыларды қамтиды. Гравитация аумағындағы адгезиясыз аққыш дененің адиабатылық ағуы жоғарғы формуладан Бернулле теңдеуін келтіріп шығарсақ болады:

Мұндағы ｐқысым күш, z санақ бетінің биіктігі. 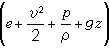формуладан бірлік массаның жалпы энаргиясын, ішкі энергиясын, кинетикалық энергиясын, қысым кұш потенциал энергиясын білуге болады. Бұл формуланың физикалық мәні: бірлік уақыт ішінде басқарушы денеге кірген және шыққан жалпы энергиялар өзара тең.

Дифференциалды форманың негізгі формулалары.Негізінен үздіксіз формула, қозғалыс формуласы, энергиялар формуласын қамтиды.

1) Үздіксіз формула. Аққыш дененің массалар сақталу заңынын шыққан. Ол тікбұрыштар координаттық жүйесінде былай өрнектеледі:

Мұндағы u, v, w-x,y,z бағыттарының жылдамдық компоненттері.

2) Қозғалыс формуласы. Бұл аққыш денелерге байланысты Ньютонның екінші заңынан келіп шыққан. Тұтқырсыз аққыш дененің қозғалыс теңдеуі ол Эйлер теңдеуі болып саналады. Ньютонның аққыш денелер теңдеуі - ол Навье – Стокс теңдеуі болып саналады.

3) Энергиялар формуласы. Ол аққыш денелердің энергиялар сақталу заңына байланысты екенін көрсететін формула. Тұтқырсыз сұйықтардың энергиялар формуласы төмендегідей:

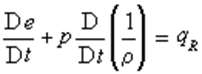
Бұл аққыш дененің ішкі энергиясының артуы мен қайтымды көлем ұлғаю жұмысының қосындысы сәулелену энергиясына тең болатынын көрсетеді. Мұндағы 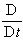кері сан бөліктің нәтижесі. Ньютонның аққыш денелер формуласы тік бұрыштар координаттар жүйесінде былай өрнектеледі.

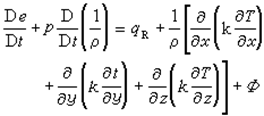
Бұл аққыш денелер ішкі энаргиясының артуы мен қайтымды көлем ұлғайту жұмысының қосындысы сәулелену энергиясына тең болатынын көрсетеді, жылу өткізгіштік және тұтқырлы ыдыратушы жұмыстың қосындысы. Мұндағы k-жылутасымалдау жылдамдығы, T-температура, Ф-ыдыратушы функция, ол бірлік уақыт ішіндегі бірлік массадағы аққыш дененің тұтқырлығы арқылы ыдырататын механикалық жұмысы, ол аққыш дененің ішкі энергиясы болып саналады. Гидродинамиканың кейбір заңдарына аэродинамика ғылымы да бағынады. Ұшақтың ұшу барысы ауа тұтқырлыңына, яғни судың орташа концентрациясында өтетіндіктен гидродинамикалық заңға бағынады.

Аэродинамика-ол газ тәрізді ортаның қозғалысының және оның акқыш денемен өзара әрекетінің зандарын зерделейтін механика ғылымы. Авиация, ракета, артиллерия кезінде кеңінен қолданылады. Аэродинамика теориялық (газ қозғалысының зандылығын және оның денеге ықпал етуін зерделейді) және эксперименттік (газ қозғалысын және оның айнала ағу денелерімен, атап айтқанда, аэродинамикалық трубалар модельдеріндегі немесе ұшу аппараттарында өзара әрекетін зерттейді) болып бөлінеді. Аэродинамиканың негізгі мақсаты — қозғалыстағы денеге газ әсер ету кезінде пайда болатын күш пен жағдайды, ұшу аппараттарының аэродинамикалық сипатқа ие болуын зерттеу.

Рейнольдс саны — инерциялық күш пен тұтқырлық күш арасындағы қатынасты зерттейтін, тұтқыр сұйықтық пен газ ағысының ұқсастық критерилерінің бірі:

Мұндағы, 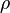-тығыздық, кг/м³; 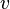- ағынның жылдамдығы, м/с; - ағынның сызықтық өлшемі, м; 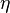-газ немесе сұйықтық тұтқырлығының динамик коэффициенті, Н·с/м². Сұйықтық ағысының режимі кризистік Рейнольдс саны (Reкр) арқылы сипатталады. Егер Рейнольдс саны өзінің кризистік мәнінен төмен болса (Re<Re_к), онда сұйықтық ағысы ламинарлық ағысқа, жоғары болса (Re>Re_к) турбуленттік ағысқа жатады. Мысалы, дөңгелек цилиндр құбырдағы тұтқыр сұйықтықтың ағысы үшін Reкр=2300 [19]. Гидромеханика және газ механикасының негізгі есептерінің, ұшақтар мен ракеталардың реактивті қозғалтқыштарында, сұйық пен газдың ағысында туатын гидравликалық кедергілерді есептеу болады. Сұйықтың қозғалысы құбырдың кіруі мен шығуында қысымның өзгерісі ықпалымен болады. Қысымның осы өзгерісінің бір бөлігі қозғалыстағы затты айдау мен көтеруге кетеді, ал басқа бөлігі әр түрлі гидравликалық кедергілерді жеңуге кетеді. Гидравликалық қысымды жеңуге жұмсалатын қысым өзгерісінің бөлімі жоғалған қысым немесе қысым шығындары Λр_пот деп аталады. Ұзындығы бойынша кедергілер құбырдың бүкіл ұзындығы бойынша гидравликалық үйкеліс түрінде бірдей бөлінген. Орташа жылдамдықтың мәні мен жылдамдықтардың бөлінуі құбырдың ұзындығы бойынша өзгермей қалса, онда қысымның таза күйдегі үйкеліске шығындары тұрақты қималы тура құбырларда сұйықтың біркелкі қозғалысында орын алады. Қысымның үйкеліске шығындары Дарси-Вейсбах формуласы арқылы анықталады:

Дата добавления: 2015-08-20