
|
Читайте также: |
Λртр=λl/dэ*ρw2/2,
мұнда λ-гидравликалық үйкеліс коэфиценті; l-құбыр ұзындығы,м.; dэ – каналдың эквиваленттік диаметрі,м.; ρ-тығыздығы, кг/м3; w-қима бойынша орташа жылдамдық, м/с.
Гидравликалық үйкеліс коэффиценті λ жалпы жағдайда Рейнольдс санына және салыстырмалы дөрекілікке Λ/d-ге байланысты болады, яғни
λ=f(Re, Λ/dэ)
мұндағы, Λ-эквиваленттік абсолюттік дөрекілік.
Бернулли теңдеуі - гидромеханиканың негізгі теңдеулерінің бірі. Бұл теңдеуді Швейцариялық ғалым Д.Бернулли (1700 —1782) өзінің 1738 жылы тұжырымдалған. Төмендегіше өрнектеледі:
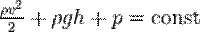
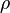 -сұйықтық тығыздығы,
-сұйықтық тығыздығы, 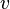 -сұйықтық жылдамдығы,
-сұйықтық жылдамдығы, 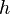 -белгілі бір горизонталь жазықтықтан бастап есептелетін сұйықтық бөлшектерінің биіктігі,
-белгілі бір горизонталь жазықтықтан бастап есептелетін сұйықтық бөлшектерінің биіктігі, 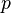 -сұйықтық қысымы,
-сұйықтық қысымы, 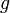 - еркін түсу үдеуі. Теңдеудің сол жағындағы алғашқы екі мүшесінің қосындысы сұйықтықтың (бірлік массаға қатысты) толық потенциалдық энергиясына, ал үшінші мүшесі сұйықтықтың кинетикалық энергиясына тең. Теңдеу қозғалыстағы сұйық ағыны үшін механикалық энергияның сақталу заңын өрнектейді.
- еркін түсу үдеуі. Теңдеудің сол жағындағы алғашқы екі мүшесінің қосындысы сұйықтықтың (бірлік массаға қатысты) толық потенциалдық энергиясына, ал үшінші мүшесі сұйықтықтың кинетикалық энергиясына тең. Теңдеу қозғалыстағы сұйық ағыны үшін механикалық энергияның сақталу заңын өрнектейді. 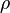 - р және һ арасындағы негізгі тәуелділікті белгілейді. Теңдеуді төмендегіше түрде де өрнектеуге болады:
- р және һ арасындағы негізгі тәуелділікті белгілейді. Теңдеуді төмендегіше түрде де өрнектеуге болады:
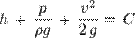 (a) және оны
(a) және оны 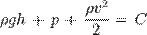 (b) деп өрнектеуге болады.
(b) деп өрнектеуге болады.
мұндағы m =  — сұйықтықтың меншікті салмағы. (a) теңдіктегі барлық қосылғыштың ұзындық өлшемдері бар және олар сәйкес түрде геометриялық, пьезометрлік және жылдамдық биіктігі деп, ал (b) теңдіктегі барлық қосылғыштың қысымдық өлшемдері бар және олар сәйкес түрде салмақтық, статикалық және динамикалық қысым деп аталады [20]. Аэродинамикалық қозғалыс егер түтікше ішінде жүрсе онда ішіндегі газ қысымы негізінен тұрақты болады.
— сұйықтықтың меншікті салмағы. (a) теңдіктегі барлық қосылғыштың ұзындық өлшемдері бар және олар сәйкес түрде геометриялық, пьезометрлік және жылдамдық биіктігі деп, ал (b) теңдіктегі барлық қосылғыштың қысымдық өлшемдері бар және олар сәйкес түрде салмақтық, статикалық және динамикалық қысым деп аталады [20]. Аэродинамикалық қозғалыс егер түтікше ішінде жүрсе онда ішіндегі газ қысымы негізінен тұрақты болады.
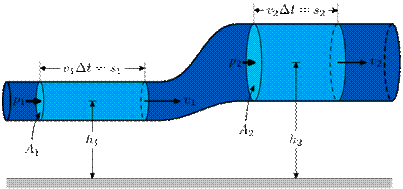
Cурет 23. Аэродинамикалық трубаның параметрлері
Аққыш дененің сыртқы күш әсерінен алынған энаргиясы:
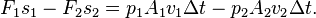
Аққыш дененің ауырлық күші әсерінен жоғалтқан энергиясы:
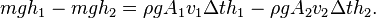
Аққыш дененің кинетикалық энергиясын былай жазуға болады:
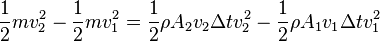
Энергиялар сақталу заңына сәйкес - аққыш дененің сыртқы күш әсерінен алынған энаргиясы + аққыш дененің ауырлық күші әсерінен жоғалтқан энергиясы = аққыш дененің жалпы кинетикалық энергиясы.
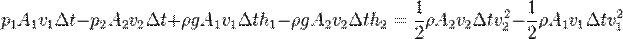
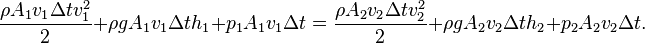
Жоғарыдағы формуладан мынаны білуге болады:
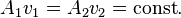 әрі
әрі 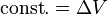 теңдеудің екі жағын
теңдеудің екі жағын 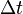 мен
мен 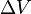 ға бөлсек:
ға бөлсек:
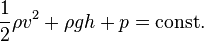
Торричелли заңы. Сұйық дене жердің тартылыс күші әсерінен ағып шығатын болса, онда жылдамдық 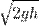 -ға тең болады.
-ға тең болады. 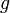 - еркін түсу үдеуі,
- еркін түсу үдеуі, 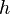 -ағып шығу аузының центр нүктесі мен сұйықтың ең жоғарғы шегі арқылы биіктікті өрнектейміз (24-сурет). Бұл жылдамдық су мен жер арасындағы биіктікпен бірдей аралықтан еркін түскен кездегі жылдамдығына тең (ауаның кедергі күшін ескермегенде).
-ағып шығу аузының центр нүктесі мен сұйықтың ең жоғарғы шегі арқылы биіктікті өрнектейміз (24-сурет). Бұл жылдамдық су мен жер арасындағы биіктікпен бірдей аралықтан еркін түскен кездегі жылдамдығына тең (ауаның кедергі күшін ескермегенде).

Сурет 24. Cұйықтың жер тартылыс күші әсерінен ағып шығуы
Идеал газ үшін төмендегі формула қолданылады:
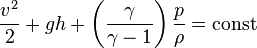
Мұндағы, 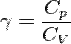 — газдың адиабаттық тұрақтысы.
— газдың адиабаттық тұрақтысы. 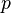 -газдың нүктедегі қысымы,
-газдың нүктедегі қысымы, 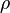 -газдың нүктедегі тығыздығы,
-газдың нүктедегі тығыздығы, 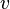 -газдың ағу жылдамдығы,
-газдың ағу жылдамдығы, 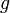 -еркін құлау үдеуі,
-еркін құлау үдеуі, 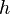 - салыстырмалы координаттар басынан биіктігі. Біртекті емес өрісте қозғалса
- салыстырмалы координаттар басынан биіктігі. Біртекті емес өрісте қозғалса 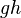 гравитациялық өріс потенциалымен алмастырылуы керек.
гравитациялық өріс потенциалымен алмастырылуы керек.
Бернулли заңының термодинамикасы.Статистикалық физикадан адиабаттық ағыста ток сызықтарында келесі шамалар тұрақты болады:
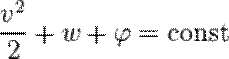
Мұндағы,  — масса бірлігінің энтальпиясы,
— масса бірлігінің энтальпиясы,  — күш потенциалы.
— күш потенциалы.
2.3 Аэродинамикалық труба
дененің ағымдылығы процесін эксперименттік зерттеу үшін ауа немесе газ ағынын жасайтын қондырғы. Үлгілерді аэродинамикалық трубада сынай отырып, жалпы ұшақтың бөліктерінің неғұрлым тиімді тұлғаларын табады, оның беріктігін, маневрлілігін, ұшу барысында оған әсер ететін жүк шамасын анықтайды. Аэродинамикалық труба өлшемдері мен ауа ағынының жылдамдығы әр түрлі болады. Аэродинамикалық труба әдетте ұшақтар, машиналар және басқа заттардың механикалық қозғалыстарын модель ретінде тәжірибеден өткізу барысында қолданылады. Рейнольдс саны бойынша жылдамдық және труба өлшемі тұтқырлыққа байланысты реттеліп отырады. Сонымен қатар, тәжірибе барысындағы аққыш дененің, мысалы ауа ағысының орташа жылдамдығы, ауаның ағу бағыты мен аэродинамика трубаның өсі арасындағы өлшем, аэродинамикалық бағыттағы газ қысым градиенті, труба ішіндегі температураның біркелкілігі, трубленттік интенсивтілік және шу дыбыстарын белгілі жүйеге түсіру қажет [21].
Құрылысы.Аэродинамикалық труба негізінен, үңгір, айналғыш парақ және өлшеу жүйесінен тұрады (25-сурет).
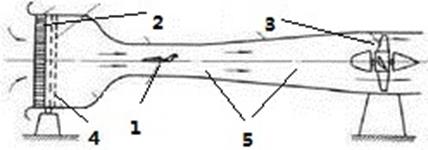
Сурет 25. Төмен жылдамдықтағы аэродинамикалық труба құрлымы
1.Өлшеу объектісі 2. Жел түзегіш тор 3. Айналу парағы 4. Орнықтырғыш 5. Үңгір
Трубада өлшеу моделіне байланысты тәжірибеде ауа ағысының ламинарлы қозғалысын жоғарылатуға болады, стабильды сегмент арқылы турбулентті қозғалысты азайтып, қалаған дәрежедегі жылдамдықты алуға болады.
Айналу парағы негізінен екіге бөлінеді:
Біріншісі, мотор группасынан, айналу парағынан немесе компрессордан құралады. Парақ айналу барысында немесе компрессор роторы айналу барысында ауа қысымына байланысты ауа ағысы біркелкі қозғалыс жасайды. Айналу парағының жылдамдығын өзгертіп немесе парақтың бұрышын өзгертіп немесе ауаның дымқылдығын өзгертіп, ауаның жылдамдығын реттеп отыруға болады. Двигательдің ұдайы тогын істету арқылы өлшеуге қолайлылық тудыруға болады.
Екінші түрі, аз энергия жұмсайтын компрессор арқылы жоғары қысымды ауаны сақтау камерасына сақтап, тәжірибе басталғанда желдің шығу клапанын ашамыз, жоғары қысым тікелей немесе эжектор арқылы үңгірге кіреді. Камера сору немесе үрлеу арқылы эжектор көмегімен жүзеге асады.
Өлшеу, басқару жүйесі.Тәжірибе барысында басқару әртүрлі клапан, қозғалыс бөлігі, модель формасы, өлешеу аспабы, сонымен қатар қысым, температура арқылы орындалады. Жылдамдық сипатқа байланысты аэродинамикалық труба дыбыс жылдамдығына дейін, трансдыбыс жылдамдықты, дыбыс жылдамдығынан жоғарғы жылдамдықта болып бөлінеді (26-сурет).

Сурет 26. Үш түрлі дыбыс жылдамдығындағы труба
1. Жел толтыру камерасы 2. Жылдам клапан 3. Қысым клапаны 4. Ұяшық 5. Кедергі торы 6. Қысаң бөлік 7. Лавар труба бөлігі 8. Тәжірибе бөлігі 9. Асқын дыбыс жылдамдық бөлігі 10. Дыбыс азайтушы 11. Дыбыс жылдамдығына дейінгі труба 12. Тәжірибе объектісі 13. Тепе теңдік бөлігі 14. Саңылау
Бұрышты датчик арқылы ауа ағысын, физикалық күштерді, форманы өлшеуге болады. Өлшеу объектісіне байланысты аэродинамикалық труба төмен жылдамдықты, жоғары жылдамдықты болып бөлінеді [22,23].
Төмен жылдамдықты труба (27-сурет) әдеттегі ұшақ қанатының кіші формасына талдау жасағанда қолданылады.

Сурет 27. Төмен жылдамдықтағы аэродинамикалық труба
Дыбыс жылдамдығына дейінгі, трансдыбыс жылдамдықты, асқын дыбыс жылдамдығындағы трубаға байланысты бұл түрдегі трубалар күрделі труба болып саналады. Олар машина сынағында және ұшақ қанатын және басқа сыртқы бөлшектерінің ауа ағысымен жанасуын зерттеуде қолданылады (28-сурет).


Сурет 28. Күрделі аэродинамикалық труба
2.4 Адгезия және когезия, беттік керілу
Жұғу дегеніміз – сұйықтықтың қатты дененің бетімен әректтесуінде жүретін физика химиялық құбылыс. Жұғуға негізгі қызмет атқаратын сұйық пен қатты дененің беттік қасиеттері. Осы ерекшелікке байланысты жұғу санының ұқсамастығы болады [24].
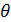 шекті бұрышы Юнг теңдеуімен анықталады. Қатты, сұйық, газ үш фазалы жүйе үшін төмендегі теңдеу орындалады.
шекті бұрышы Юнг теңдеуімен анықталады. Қатты, сұйық, газ үш фазалы жүйе үшін төмендегі теңдеу орындалады.
Cos 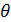 =(
=(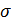 кг-
кг- 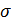 кс)/
кс)/ 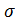 сг
сг
Юнг заңы капиллярлық құбылыстардың негізгі заңы болып есептеледі. Сондықтан оны капиллярлықтың екінші заңы деп атауға болады. Көлемі V болатын жазық бетке қондырылған тұрақты тамшының жұғу сызығын dr қашықтыққа жылжытып, беттік энергиясының өзгерісін есептесек, сұйық жұққан аудан 2 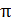 rdr шамасына өзгереді. Жұғу сызығының жылжуы тамшының газ арасындағы беттік ауданның Sсг өсуіне де әкеледі. Жазық бетте тамшы сфералық сегмент формасында болады, сондықтан тамшының беткі ауданының ұлғаюы dsсг =2
rdr шамасына өзгереді. Жұғу сызығының жылжуы тамшының газ арасындағы беттік ауданның Sсг өсуіне де әкеледі. Жазық бетте тамшы сфералық сегмент формасында болады, сондықтан тамшының беткі ауданының ұлғаюы dsсг =2 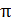 rdl, dl= Cos
rdl, dl= Cos 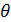 dr- AC
dr- AC
Сұйық-газ шекарасындағы беттік энергия 2 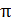 r
r 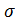 сг Cos
сг Cos 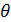 dr шамасына ұлғаяды. Яғни, термодинамикалық тепе-теңдіктің шарты келесі теңдеумен анықталады:
dr шамасына ұлғаяды. Яғни, термодинамикалық тепе-теңдіктің шарты келесі теңдеумен анықталады:
(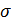 кг-
кг- 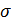 кс) 2
кс) 2 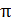 rdr+2
rdr+2 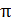 r
r 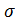 сг Cos
сг Cos 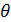 dr=0
dr=0
Осы теңдеуден Юнг теңдеуі шығады. Юнг заңына сүйене отырып, қатты бет пен сұйықтық арасындағы әрекеттесуді жіктеуге болады.
Жұқпау, (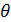 >900) бұл жағдайда қатты дене мен газ шекарасындағы беттік керілуге
>900) бұл жағдайда қатты дене мен газ шекарасындағы беттік керілуге 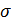 кг қарағанда, қатты дене сұйықтық шекарасындағы меншікті бет энергиясы
кг қарағанда, қатты дене сұйықтық шекарасындағы меншікті бет энергиясы 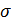 кс артық болады. Сол себепті қатты дене бетіне сұйықтық өздігінен жайылмайды. Юнг заңынан жұқпау шарттары шығады.
кс артық болады. Сол себепті қатты дене бетіне сұйықтық өздігінен жайылмайды. Юнг заңынан жұқпау шарттары шығады.
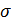 кс>
кс> 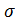 кг, Cos
кг, Cos 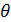 <0,
<0, 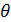 >900
>900
Сұйықтар жұқпайтын беттер әдетте лиофобты бет деп аталады. Ал су жұқпайтын бетті гидрофобты бет деп атаймыз. Жұғу әдетте, 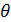 < 900 бұл жағдайда қатты дененің газбен шекарасындағы беттік керілуге қарағанда
< 900 бұл жағдайда қатты дененің газбен шекарасындағы беттік керілуге қарағанда 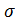 кг қатты дене мен сұйық арасындағы энергиясы
кг қатты дене мен сұйық арасындағы энергиясы 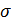 кс аз болады. Юнг заңына сәйкес жұғу шарттары:
кс аз болады. Юнг заңына сәйкес жұғу шарттары:
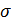 кс<
кс< 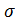 кг, Cos
кг, Cos 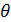 >0,
>0, 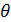 <900
<900
Юнг теңдеуіне кіретін 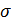 кс,
кс, 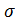 кг шамалары белгісіз болғандықтан
кг шамалары белгісіз болғандықтан 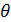 бұрышын анықтайтын молекулярлық күштер мен олардың жұмысын қарастыру керек. Бір фазаның молекулаларының арасындағы когезия күштері деп, ал әртүрлі фаза арасындағы тартылу күшін адгезия деп атаймыз. Осыған сәйкес когезия жұмысы деп біртүрлі көлемдік фазаны бөлу үшін жұмсалған жұмысты айтамыз. Мұндай жұмыс төмендегідей болады:
бұрышын анықтайтын молекулярлық күштер мен олардың жұмысын қарастыру керек. Бір фазаның молекулаларының арасындағы когезия күштері деп, ал әртүрлі фаза арасындағы тартылу күшін адгезия деп атаймыз. Осыған сәйкес когезия жұмысы деп біртүрлі көлемдік фазаны бөлу үшін жұмсалған жұмысты айтамыз. Мұндай жұмыс төмендегідей болады:
Wc=2 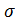 сг
сг
Себебі сұйық газ екі беті түзіледі.
Адгезия жұмысы дегеніміз – фазааралық беттік қабатты бұзу үшін жұмсалған жұмыс [24]. Ол екі жаңа беттің түзілуіне жұмсалады. Ал бастапқы беттің бос энергиясы жойылып, қатты сұйық шекарасы үшін адгезия жұмысы төмендегіндей болады:
Wa= 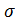 сг+
сг+ 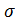 кг-
кг- 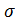 кс
кс
Бұл теңдеу бойынша қатты сұйық шекарасындағы Wa фазааралық әрекеттесудің күшеюі мен фазааралық керілу 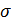 кс кемиді. Юнг заңын қолдана отырып, Дюпре теңдеуін шығаруға болады:
кс кемиді. Юнг заңын қолдана отырып, Дюпре теңдеуін шығаруға болады:
Wa= 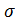 сг(1+ Cos
сг(1+ Cos 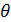 )
)
Бұл теңдеуден 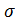 сг, Cos
сг, Cos 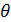 эксперименттік мәндері арқылы Wa шамасын анықтауға болады. Адгезия артса жұғу жоғары болады.
эксперименттік мәндері арқылы Wa шамасын анықтауға болады. Адгезия артса жұғу жоғары болады.
2.5 Супергидрофобты беттің физикалық негізі
Қатты дене мен су арасында сұйықтың беттік керілу қасиетіне, қатты дененің беттік құрлымына байланысты қатты дене беті гидрофильді және гидрофобты болып бөлінеді. Ал гидрофобты дәрежесіне байланысты гидрофобты және супергидрофобты материал болып бөлінеді. [24,25]. Гидрофобты қасиет қатты дене мен су арасындағы бір бірін тебу жағдайын көрсетеді. Дене бетіне судың жұғуы негізінен үш түрлі болады (29-сурет).
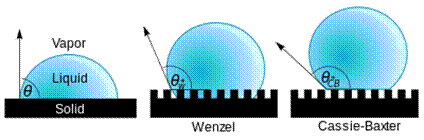
Сурет 29. Cудың қатты бетке жұғу жағдайлары. Түрлері:
1. Жазық беттегі 2. Wenzel моделі 3. Cassie's –baxter моделі.
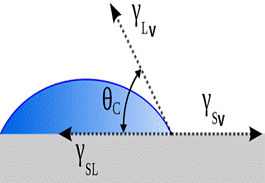
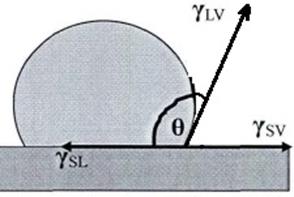
Гидрофильді бет Гидрофобты бет
Сурет 30. Әр фаза арасындағы беттік керілулері
Әр түрлі теңдеулер бойынша қатты беттің гидрофобты, гидрофильді екенін ажыратуға болады.
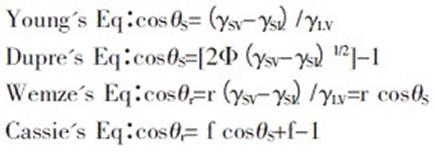
Мұндағы, γSL, γSV, γLV қатты-сұйық, қатты-газ, сұйық-газ беттік керілулері. Φ-тұрақты коэффициент, θS-жазық беттегі жанасу бұрышы, θr-дөрекі беттегі жанасу бұрышы, r-дөрекілік факторы, f-сұйықтың қатты беттегі аудандық үлесі. Қатты дененің гидрофильді немесе гидрофобты болуы оның бетіндегі екінші реттік құрлымға байланысты болады. Гидрофильді қатты беттің құрлымы екінші реттік топшарлардың болмауы немесе топшалар диаметрінің үлкен болу себептері. Ал гидрофобты беттің физикалық құрлымы дөрекі екінші беттік құрылымнан тұрады (31-сурет). Дөрекілік топшалар капиллярлық қысым тудырады, сондықтан гидрофобты қасиетке ие болады [26].


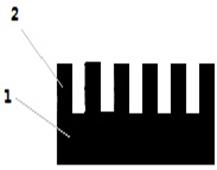
Cурет 31. Гидрофобты беттің құрылымы
1. Негізгі бет 2. Екіншілік құрылым
Беткі қабатта капиллярлы қысым пайда болады. Капиллярлы қысым әсерінен тамшы бетке жайылмай шар формасын сақтап тұрады [27].
Капиллярлы қысым және Юнг –Лаплас ортақ теңдеуі
Капиллярлық қысым – судың капилляр бойымен көтерілу шамасын көрсететін қысым, яғни диаметрге байланысты және сұйықтың беттік керілу қасиетіне байланысты сұйықтың жоғары көтерілуі. Егер сұйықтың когезия күші адгезия күшінен үлкен болса, онда капилляр бойымен жоғары көтерілмейді, ал егер адгезия жұмысы когезия жұмысынан көп болса, онда сұйықтың дене бетіне жұғуы байқалады, капилляр бойымен жоғары көтеріледі (32-сурет).

Cурет 32. Капиллярлық қысымның беттік керілуге байланысы
Лаплас теңдеуі сызықты емес теңдеу болып саналады. Екі тыныш күйдегі аққыш дене арасындағы беттік керілу немесе қабырғаға керілуінен шыққан капиллярлық қысымның айырмасынан шыққан, мысалы, су мен ауа. Лаплас теңдеуі қысым айырмасы мен беттік құрлымды байланыстырады [27]. Тыныш күйдегі капилляр бетін зерттеуге қолайлылық тудырады. Формула сұйықтық интерфейсінің қысым тепе-теңдігін түсіндіреді (интерфейс қалыңдығы нольге тең).
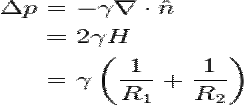
Мұндағы, 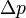 -интерфейс арасындағы қысым айырмасы, γ-беттік керілу коэффициенті,
-интерфейс арасындағы қысым айырмасы, γ-беттік керілу коэффициенті, 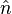 -интерфейс сыртына бағытталған вектор,
-интерфейс сыртына бағытталған вектор, 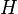 -орташа кривизна,
-орташа кривизна, 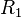 және
және 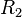 кривизналық радиус, негізінен оң қысым күшті қарастырады. Қысым күш айырмасы:
кривизналық радиус, негізінен оң қысым күшті қарастырады. Қысым күш айырмасы:
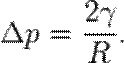
Әдетте, су тамшысының радиусы жанасу бұрышының функциясы болып табылады (33-сурет).
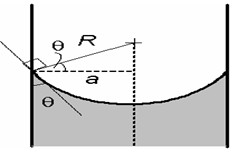
Сурет 33. Жұғу бұрышының радиуспен қатысы
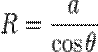
Қысым айырмасын былай жазуға болады.
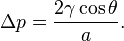
Сұйықтық тепе-тең болған кезде, h оң немесе теріс мән алуы мүмкін. Яғни, жанау бұрышының 900 -тан үлкен немесе кіші екенін көрсетеді. Әрі аққыш дене тығыздығына байланысты:
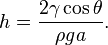
Әдеттегі жағдайда қысым айырмасы ΔP сұйқтық қысымы мен сыртқы қысым әсерінен Юнг –Лаплас теңдеуі төмендегідей болады:
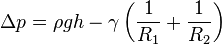
Бұл формуладан капилляр ұзындығын былай деп өрнектеуге болады:
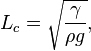
Қысымның сипаттамасы:
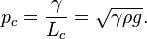
Таза су әдетте қалыпты температура мен қалыпты қысымда капилляр ұзындығы 2 mm болады. Ал өлшемсіз формуласы төмендегіше болады.
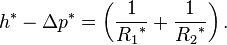
Супергидрофобты беттің беткі қабатында да капиллярлық қысым жоғары болады. Екінші реттік құрылымдар, яғни, өсінділер өзара шеңбер құрайды (34-сурет).
Дата добавления: 2015-08-20; просмотров: 444 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| РЕФЕРАТ 2 страница | | | РЕФЕРАТ 4 страница |