Представление сигналов рядом Фурье

Теорема Фурье: Любая периодическая функция 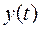может быть представлена в виде суммы ряда составляющих, из которых одна составляющая постоянная, а другие являются синусоидальными функциями с кратными частотами (гармонические составляющие или просто гармоники).

Все сигналы электросвязи имеют сложную форму и их математические модели представляются сложными выражениями. Для упрощения расчетов цепей при негармоническом воздействии используют представление функций сложной формы с помощью суммы простых функций. Сущность этого представления состоит в следующем: Любой электрический сигнал 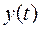с периодом 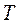на произвольно заданном интервале времени можно записать в виде суммы простых гармонических колебаний вида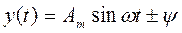

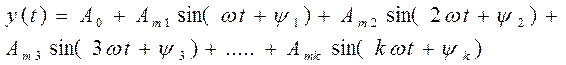
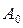- постоянная составляющая;

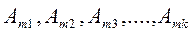-амплитуды гармонических составляющих;

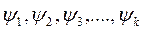-начальные фазы гармоник.

Первая гармоническая составляющая имеет период, равный периоду несинусоидального сигнала и называется первой или основной гармоникой. Все другие составляющие имеют частоты в целое число раз больше частоты первой гармоники и называются высшими.

Пример

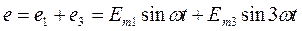
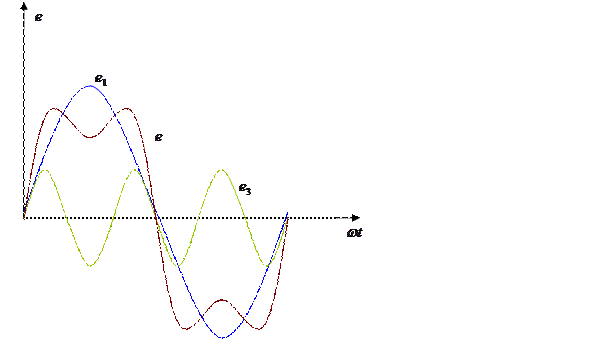
Тригонометрический ряд после раскрытия синуса суммы для каждой гармоники записывается в следующем виде:

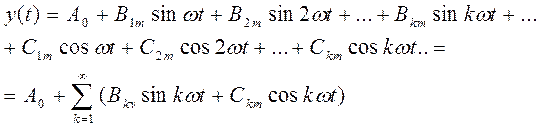
Преобразование выполнили, применив формулу синуса суммы двух углов. Обозначив постоянные величины

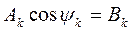и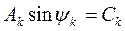

Коэффициенты 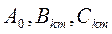Могут быть вычислены при помощи следующих интегралов:

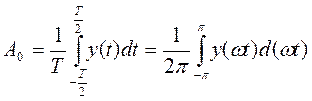
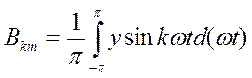
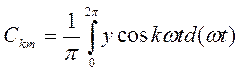
Таким образом, мгновенные значения любого периодического негармонического сигнала записывается в виде математического выражения, представляющего сумму гармонической составляющих и постоянной составляющей, известного под названием ряда Фурье.

Дата добавления: 2015-08-20