Читайте также:
|
Пусть имеется связанная система, в которой можно изменять резонансную частоту и значение связи между контурами. Заменим двухконтурную схему эквивалентной одноконтурной. Где 
и 
- активное и реактивное сопротивления первого контура, а 
и 
- вносимые активное и реактивное сопротивления, учитывающие потери активной и реактивной мощностей во вторичном контуре.
, 
Изменяя связь между катушками, можно найти значение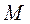 
, при котором ток во вторичном контуре достигает наибольшего значения. Ток во вторичном контуре достигает максимального значения, если 
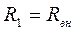. Такое значение 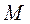называется оптимальным.
При резонансе ток во входной цепи совпадает по фазе с входным напряжением, что возможно при условии 
, что является условием резонанса в связанной системе. Данное условие выполняется в двух случаях:
1. Каждый контур расстроен, но . Такой резонанс называется сложным. Это достигается при значении взаимной индуктивности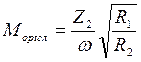 
2. Каждый контур настроен в резонанс, т.е. 
. Такой резонанс называется основным или индивидуальным. Значение взаимной индуктивности 
3. Каждый контур настроен в резонанс, т.е. 
. Такой резонанс называется полным и является частным случаем основного.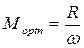 
Дата добавления: 2015-08-20; просмотров: 133 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Коэффициент связи | | | Параметр связи |