Простейшие движений твердого тела

Следующей по сложности моделью после частицы является абсолютно твердое тело - в нем расстояние между любыми двумя точками не меняется в процессе движения.

Описание движения твердого тела кроме самостоятельного значения имеет большое значение и в применении к описаниям других видов движения. Система отсчета, служащая для пространственно-временного описания различных движений может быть связана только с твердым телом. Поэтому изучение движения твердых тел равносильно изучению движений систем отсчета. Результаты этого раздела будут неоднократно использоваться в дальнейшем.

Имеется пять видов движения твердого тела:

1) поступательное, если прямая, соединяющая любые две точки тела, перемещается, оставаясь параллельной своему начальному положению, например движение трамвая на прямом участке пути;

2) вращательно е, если все точки лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными, например движение двери при открывании и закрывании;

3) плоское, если все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета, например качение колеса на прямом участке пути;

4) сферическое, если одна из точек тела остается все время неподвижной в рассматриваемой системе отсчета, например движение гироскопа с тремя степенями свободы в карданном подвесе;

5) свободное, если нет перечисленных выше четырех ограничений, например движение свободного произвольного брошенного тела вблизи поверхности Земли.

Первые два движения являются основными движениями твердого тела. Остальные виды движения твердого тела можно свести к одному из основных движений или к их совокупности (это будет показано на примере плоского движения).

В этом разделе рассмотрим первые три вида движения и вопрос сложения угловых скоростей.

При поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной частицы тела, т. е. к задаче кинематики частицы. Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус-вектора 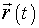любой точки этого тела и его положение в начальный момент, как это было описано в предыдущем разделе.

Рассмотрим вращение вокруг неподвижной в данной системе отсчета Рис. 2.6. Вращение твердого тела вокруг неподвижной оси

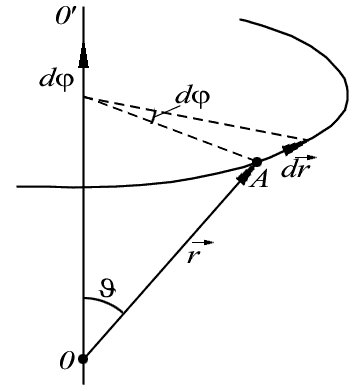
оси 00'. Пусть твердое тело, вращаясь вокруг нее, совершило за время dt бесконечно малый поворот. Угол поворота будем характеризовать вектором 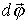, модуль которого равен углу поворота 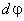, а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора 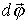(рис. 2.6). Вектор 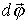называется аксиальным вектором, тогда как вектор перемещения 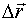является полярным вектором (к ним также относятся векторы скорости и ускорения). Они отличаются тем, что полярный вектор кроме длины и направления имеет точку приложения (полюс), а аксиальный вектор имеет только длину и направление (ось - по латыни axis), но не имеет точки приложения. Векторы такого типа часто применяются в физике. К ним, например, относятся все векторя, являющиеся векторным произведением двух полярных векторов.

Найдем элементарное перемещение любой частицы А твердого тела при таком повороте. Положение частицы А зададим радиус-вектором 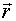, проведенным из некоторой точки О на оси вращения. Тогда линейное перемещение конца радиус-вектора 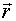связано с углом поворота 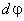соотношением (рис. 2.6)

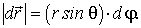
или в векторном виде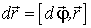

Заметим, что это равенство справедливо лишь для бесконечно малого поворота 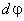, то есть только бесконечно малые повороты можно рассматривать как векторы. Для конечного поворота на угол 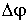линейное перемещение частицы А определяется формулой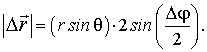

Очевидно, что перемещение 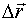нельзя представить как векторное произведение векторов 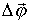и 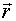, так как это возможно лишь при бесконечно малом повороте 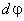, когда радиус-вектор 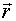можно считать неизменным.

Можно показать, что введенный вектор 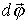удовлетворяет основному свойству векторов - векторному сложению. Пусть твердое тело совершает два элементарных поворота 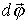₁ и 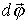₂ вокруг разных осей, проходящих через неподвижную точку О. Тогда суммарное перемещение 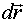произвольной частицы А тела, радиус-вектор которой относительно точки О равен 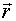, можно представить так:

,

где

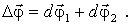
Мы доказали, что два поворота, 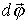₁ и 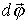₂, эквивалентны одному повороту на угол 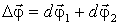вокруг оси, совпадающей с вектором 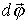и проходящей через точку О.

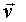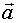Введем теперь векторы угловой скорости и углового ускорения таким же способом, как мы вводили векторы и . Вектор угловой скорости 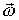определяют так

где dt - интервал времени, за который тело совершает поворот 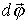. Вектор 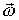совпадает по направлению с вектором 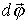и является аксиальным вектором.

Изменение вектора 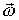со временем характеризуют вектором углового ускорения 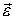, который определяют соотношением

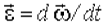
Направление вектора 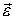совпадает с направлением 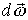- приращения угловой скорости 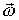. Вектор 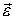, как и 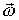, также аксиальный.

Представление угловой скорости и углового ускорения в виде векторов очень полезно при изучении более сложных движений твердого тела. Это позволяет во многих случаях получить большую наглядность, а также резко упростить как анализ движения, так и соответствующие расчеты.

Представим выражения для угловой скорости и углового ускорения в проекциях на ось вращения Оz, положительное направление которой свяжем правилом правого винта с положительным направлением отсчета координаты (-угла поворота- (рис. 2.7). 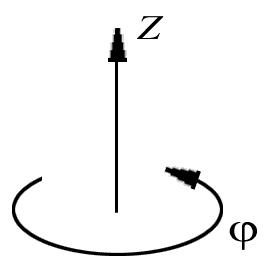Рис. 2.7.
Введение понятия угловых векторов

Тогда проекци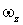и и 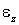векторов 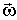и 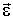на ось определяются формулами: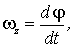

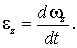
В этих формулах 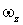и 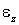- алгебраические величины. Их знак характеризует направление соответствующего вектора. Например, если 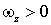, то направление вектора 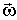совпадает с положительным направлением оси z. Если 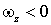, то и направление вектора 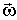противоположно. Аналогично правило верно для углового ускорения.

По известной зависимости 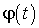, называющейся законом вращения тела, формулы (2.15) и (2.16) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости 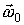и угла (₀ в начальный момент времени, можно найт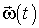и и .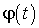

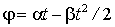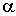Пусть твердое тело вращается вокруг неподвижной оси по закону , где и 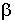- некоторые положительные постоянные. Определим движения тела.

Согласно (2.15) и (2.16), 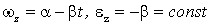. Из этих соотношений видно, что тело вращается равнозамедленно (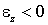), останавливается в момент времени 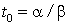, а затем начинает вращаться в противоположном направлении ().

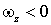Легко заметить, что все задачи на вращение твердого тела вокруг неподвижной оси аналогичны по форме задачам на прямолинейное движение частицы. Достаточно заменить линейные величины x, 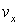и 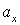на соответствующие угловые , 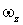и 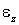, как получаются все закономерности и соотношения для вращающегося тела.

Установим связь между линейными и угловыми величинами.

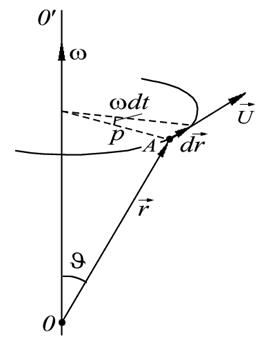
Рис. 2.8.
Связь линейных и угловых величин при вращении

Определим вектор скорости 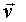произвольной частицы А твердого тела, вращающегося вокруг неподвижной оси 00' с угловой скоростью 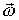. Пусть положение точки А относительно некоторой точки О оси вращения характеризуется радиус-вектором 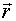(рис. 2.8).

Если формулу (2.11) поделить на промежуток времени dt, то так как 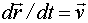и 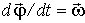), получим

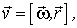
т. е. скорость 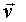любой частицы А твердого тела, вращающегося вокруг некоторой оси с угловой скоростью 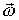, равна векторному произведению 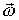на радиус-вектор 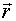частицы А относительно произвольной точки О оси вращения (рис. 2.8). Модуль вектора 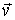(2.17) 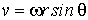, или , где R- радиус окружности, по которой движется точка А. Дифференцирование равенства (2.17) по времени дает ускорение 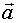частицы А: 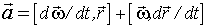, т.е.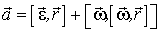

Так как в рассматриваемом случае ось вращения неподвижна, то угловая скорость 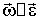, поэтому первое слагаемое в (2.18) представляет собой тангенциальное ускорение 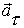, а второе слагаемое - это нормальное ускорение 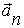. Модули этих ускорений равны: 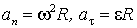, отсюда модуль полного ускорения a равен .

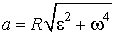Следующим по сложности является плоское движение - это такое движение, при котором каждая точка твердого тела движется в плоскости, параллельной некоторой неподвижной в данной системе отсчета плоскости. Плоская фигура Ф, образованная сечением тела этой неподвижной плоскостью Р (рис. 2.9)

,

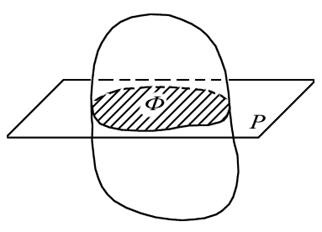
Рис. 2.9.
Определение плоского движения

в процессе движения все время остается в этой плоскости. Примером может служить цилиндр, катящийся по плоскости без скольжения.

Положение твердого тела при плоском движении однозначно определяется положением плоской фигуры Ф в неподвижной плоскости Р. (рис. 2.9). Это позволяет свести изучение плоского движения твердого тела

к изучению движения плоской фигуры в ее плоскости. Пусть плоская фигура Ф движется в своей плоскости Р, неподвижной в рассматриваемой системе отсчета К.

Положение фигуры Ф на плоскости можно определить, задав радиус-вектор 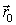произвольной точки О' фигуры и угол (между радиус-вектором 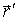, жестко связанным с фигурой, и некоторым фиксированным направлением. Тогда плоское движение твердого тела будет описываться двумя уравнениями:

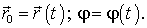
Если за промежуток времени dt радиус-вектор 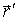частицы А (рис. 2.10) повернется на угол 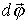, то на такой же угол повернется и любой отрезок,

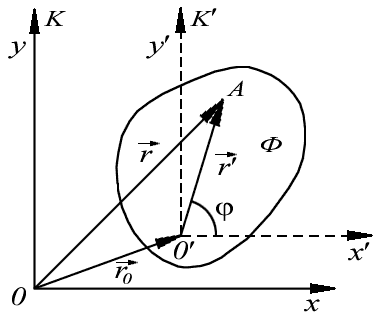
Рис. 2.10.
Плоское движение твердого тела

связанный с фигурой, так как она есть сечение твердого тела.

Отсюда видно, что поворот фигуры на угол 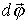не зависит от выбора точки 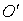, следовательно и угловая скорость 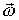фигуры тоже не зависит от выбора точки 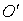, и мы имеем право называть 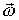угловой скоростью всего твердого тела.

Определим скорость 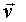произвольной частицы А тела при плоском движении. Введем вспомогательную систему отсчета K', жестко связаннyю с точкой 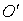тела и перемещающуюся поступательно относительно K-системы (рис. 2.10). Тогда малое перемещение 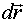частицы А в системе К можно записать как сумму векторов

,

где 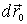- перемещение точки 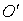, a 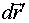- перемещение точки А относительно системы K'. Перемещение 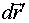вызвано вращением тела вокруг неподвижной в K-системе оси, проходящей через точку 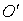согласно (2.11), 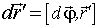. После подстановки этого выражения и деления обеих частей предыдущего равенства на dt, получим

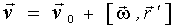
т. е. скорость произвольной частицы А твердого тела при плоском движении складывается из скорости 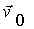произвольной точки О' этого тела и скорости 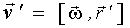вращения тела вокруг оси, проходящей через эту точку. Соотношение (2.19) справедливо и для произвольного сложного движения твердого тела. Заметим, что 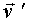- это скорость частицы А относительно поступательно движущейся системы отсчета, жестко связанной с точкой .

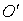Итак, доказано, что плоское движение твердого тела можно представить как совокупность двух основных видов движения - поступательного (вместе с произвольной точкой 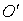тела) и вращательного (вокруг оси, проходящей через точку 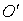). Так как кинематика - это геометрическое описание свойств движения тела, то для доказательства этого утверждения можно использовать известную теорему из геометрии, которая утверждает, что любое преобразование на плоскости, оставляющее фигуру неизменной, может быть представлено в виде комбинации параллельного переноса и вращения.

Докажем, что плоское движение можно представить как чистое вращение. Действительно, при плоском движении скорость 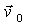произвольной точки 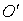тела перпендикулярна вектору 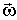, а это значит, что всегда есть такая жестко связанная с телом точка М, не обязательно принадлежащая телу, скорость которой 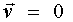в данный момент. Из условия 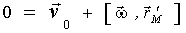можно найти радиус-вектор точки М: 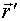_М относительно точки О' (рис. 2.11).

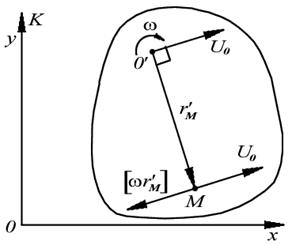
Рис. image2.11.
Мгновенная ось вращения

Вектор 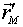перпендикулярен векторам 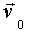и 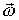, лежит в плоскости движения, а его модуль 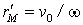. Точка М определяет положение оси вращения, совпадающей по направлению с вектором 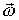. Движение твердого тела в данный момент времени представляет собой чистое вращение вокруг этой оси, которую называют мгновенной осью вращения. Положение мгновенной оси со временем меняется. Например, у катящегося по плоскости цилиндра мгновенная ось в каждый момент совпадает с линией касания цилиндра и плоскости.

Сложение угловых скоростей. Рассмотрим движение твердого тела, вращающегося одновременно вокруг двух пересекающихся осей. Пусть некоторое тело вращается с угловой скоростью 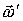вокруг оси ОА (рис. 2.12).

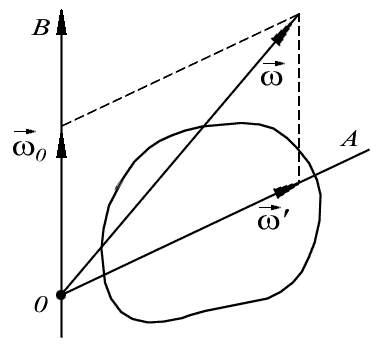
Рис. 2.12.
Сложение угловых скоростей

Приведем эту ось во вращение с угловой скоростью 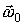вокруг другой оси ОВ, неподвижной в К-системе отсчета. Определим результирующее движение тела в ней. Для этого рассмотрим вспомогательную К'-систему отсчета, жестко связанную с осями ОА и ОВ. Эта система вращается с угловой скоростью 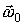, и тело вращается относительно нее с угловой скоростью 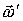. За интервал времени dt тело совершит поворот вокруг оси ОА в К'-системе и одновременно поворот 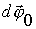вокруг оси 0В вместе с К' -системой. Итоговый поворот будет равен сумме 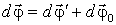. Поделив обе части этого равенства на dt, получим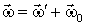

Результирующее движение твердого тела в К-системе представляет собой чистое вращение с угловой скоростью 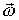вокруг оси, совпадающей в каждый момент с вектором 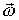и проходящей через точку 0 (рис. 2.12). Эта ось перемещается относительно К-системы - она поворачивается с угловой скоростью 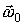вместе с осью О А вокруг оси ОВ. Даже в случае, когда угловые скорост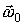и и 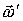не меняются по величине, тело будет обладать в К-системе угловым ускорением 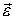, направленным перпендикулярно плоскости (рис. 2.12)

Так как вектор угловой скорости 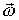удовлетворяет основному свойству векторов - векторному сложению, то его можно представить как векторную сумму составляющих, т.е. 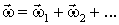, где все векторы относятся к одной и той же системе отсчета. Этот удобный и полезный способ часто применяется для анализа сложного движения твердого тела.

Дата добавления: 2015-08-20