Метод Даламбера

Сущность метода Даламбера заключается в составлении менее комплексного уравнения (32.4) в случае посредством замены переменных чтобы образованное после замены новое уравнение из вторых производных включало в себя только смешанную производную.

Предположим, что необходимо найти решение задачи Коши для бесконечной струны:

(33.1)

(33.2)

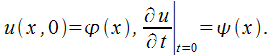
Найдем решение с помощью метода Даламбера. Характеристическое уравнение Следовательно,

или

В (33.1) осуществим замену переменных:

В этом случае

Последнее уравнение может быть также обозначено в виде

или

получается, что предполагает зависимость только от , а 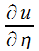зависит только от

Следовательно,

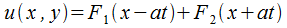
представляет собой общее решение уравнения (33.1). Данное решение именуется решением Даламбера. Для определения функций применим исходные условия (33.2), а также используем производную

В результате имеем систему

Осуществим интегрирование второго равенства в пределах от 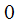до :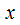

Применяя первое равенство, получаем

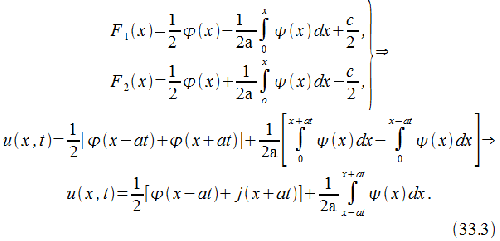
Дата добавления: 2015-08-20