
|
Читайте также: |
(результаты вычислений внести в таблицы 4.1.1 и 4.1.2)
1) Используя формулу, выражающую определение электрического сопротивления, выразить через показания вольтметра U из и амперметра J из и вычислить общее сопротивление 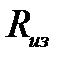 соединенных последовательно проводника и амперметра (схема 1).
соединенных последовательно проводника и амперметра (схема 1).
2) Используя формулу, выражающую определение электрического сопротивления, выразить через показания амперметра J из и вольтметра U из и вычислить общее сопротивление соединенных параллельно проводника и вольтметра R из (схема 2).
3) Используя формулы общего напряжения, общей силы тока при последовательном соединении проводников и формулу, выражающую определение сопротивления проводника, получить выражение сопротивления проводника R x через сопротивление амперметра R A, показание вольтметра U из и показание амперметра J из (схема 1):
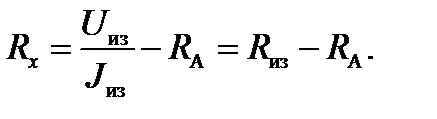 .
.
4) Используя формулы общей силы тока, общего напряжения при параллельном соединении проводников и формулу, выражающую определение сопротивления
проводника, получить выражение сопротивления проводника через сопротивление вольтметра RV, показание амперметра J из и показание вольтметра U из (схема 2):
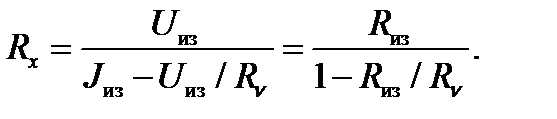
5) Вычислить сопротивления R x проводников на основе экспериментальных данных U из, J из и сопротивлений амперметра R A и вольтметра R v по схемам 1 и 2.
6) Вычислить среднее значение сопротивлений R x1 и R x2, определенных по схемам 1 и 2:
R c = 0,5 (R x1 + R x2),
и принять его за истинное значение сопротивления проводника.
7) Вычислить разницу Δ R сопротивления проводника R c от сопротивлений R из, определенных по показаниям приборов по схеме 1 и по схеме 2:
Δ R = R с– R из.
8) Вычислить относительное отличие сопротивлений R из от среднего значения сопротивления Rc: 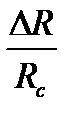 .
.
9) Используя формулу сопротивления цилиндрических проводников и геометрические размеры проводника, выразить через среднее значение сопротивление RC и диаметр и длину проволоки D и  и вычислить удельное сопротивление материала проводника r:
и вычислить удельное сопротивление материала проводника r:
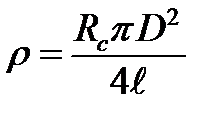 .
.
10) Вычислить среднее значение удельного сопротивления материала проводника 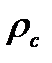 .
.
11) Сопоставив  с табличными значениями удельных сопротивлений металлов, определить материал, из которого изготовлен проводник.
с табличными значениями удельных сопротивлений металлов, определить материал, из которого изготовлен проводник.
12) Используя связь удельного электрического сопротивления 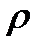 с удельной электропроводностью материала g, вычислить g.
с удельной электропроводностью материала g, вычислить g.
13) Используя формулу, выражающую определение плотности тока j, получить выражение плотности тока через силу тока J и D:
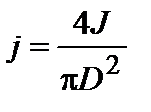 .
.
14) Вычислить плотность тока при одной из выбранных длин проводника.
15) Используя формулу закона Ома в дифференциальной форме, вычислить напряженность электрического поля в проводнике Е при определенной в задании 14 плотности тока j.
16) Принимая электрическое поле внутри проводника однородным,
учитывая, что напряжение совпадает с разностью потенциалов на концах проводника,
используя связь напряженности электрического поля с разностью потенциалов,
вычислить напряженность 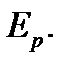
17) Выбрав в качестве точки проводника бесконечно малый цилиндрик с высотой 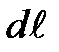 и площадью основания
и площадью основания 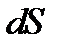 , определения плотности тока и силы тока,
, определения плотности тока и силы тока,
используя выражение электрического заряда через объемную плотность 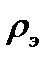 ,
,
используя выражение 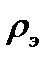 через концентрацию
через концентрацию 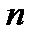 и заряд
и заряд 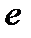 свободных переносчиков заряда,
свободных переносчиков заряда,
используя формулу объема цилиндра,
учитывая, что по определению модуль скорости упорядоченного движения переносчиков заряда 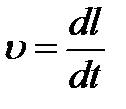 ,
,
получить выражение плотности тока через 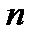 ,
, 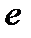 ,
, 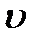 :
:
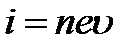 .
.
18) Принимая, что на каждый атом металла приходится один свободный электрон, а концентрация электронов 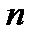 равняется концентрации атомов металла, и, учитывая определения концентрации
равняется концентрации атомов металла, и, учитывая определения концентрации 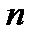 , плотности вещества
, плотности вещества 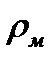 и выражения молярной массы
и выражения молярной массы 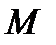 через число Авогадро
через число Авогадро 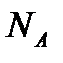 , получить выражение
, получить выражение 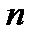 через
через 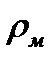 ,
, 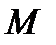 и
и 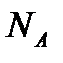 :
:
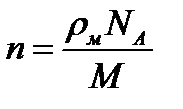 .
.
19) Принимая, что провод изготовлен из сплава фехраль (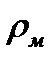 =7,8 . 103кг/м3,
=7,8 . 103кг/м3, 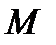 =0,056 кг/моль,
=0,056 кг/моль, 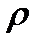 =1,3 . 10-8 Ом . м), вычислить концентрацию переносчиков заряда
=1,3 . 10-8 Ом . м), вычислить концентрацию переносчиков заряда 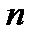 .
.
20) Используя выражение плотности тока j через характеристики переносчиков заряда, вычислить скорость упорядоченного движения электронов  при выбранной в задании 14 силе тока J.
при выбранной в задании 14 силе тока J.
21) Рассматривая совокупность обобществленных электронов в металлах как идеальный газ и используя связь кинетической энергии теплового хаотичного движения электронов с абсолютной температурой, получить выражение средней скорости теплового хаотичного движения электронов через постоянную Больцмана к, массу электрона mе и абсолютную температуру Т:
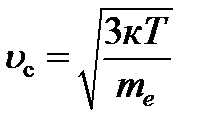 .
.
22) Используя табличные значения к, m, и пренебрегая нагреванием проводника при прохождении тока по нему, вычислить среднюю скорость 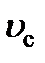 теплового движения электронов в металле при комнатной температуре Т и сравнить
теплового движения электронов в металле при комнатной температуре Т и сравнить 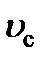 со скоростью упорядоченного движения электронов в металле
со скоростью упорядоченного движения электронов в металле 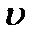 (см. задание 20).
(см. задание 20).
23) Рассматривая электрон в проводнике как свободную частицу
используя формулу силы, с которой электрическое поле действует на электрический заряд,
формулу второго закона Ньютона,
принимая, что между столкновениями электрон двигается равноускоренно с начальной скоростью 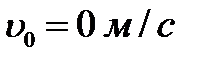 , используя формулы скорости и средней скорости при равноускоренном движении,
, используя формулы скорости и средней скорости при равноускоренном движении,
используя формулу, выражающую плотность тока через характеристики переносчиков заряда,
вывести формулу закона Ома в дифференциальной форме согласно классической электронной теории электропроводности металлов:
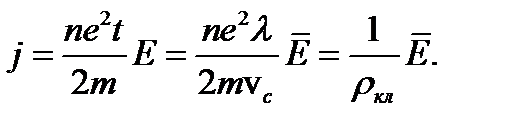
24) Принимая за 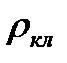 удельное электрическое сопротивление
удельное электрическое сопротивление 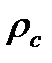 (см. задание 10) и используя табличные значения mе, e, вычислить среднюю длину свободного пробега электрона в проводнике
(см. задание 10) и используя табличные значения mе, e, вычислить среднюю длину свободного пробега электрона в проводнике 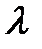 при комнатной температуре Т:
при комнатной температуре Т:
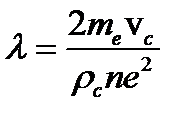 .
.
25) Сравнить длину свободного пробега электрона 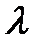 с расстоянием
с расстоянием 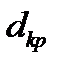 между узлами кристаллической решетки (с постоянной кристаллической решетки).
между узлами кристаллической решетки (с постоянной кристаллической решетки).
Таблица 4.1.1
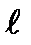
| Номер схемы | 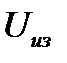 В
В
| 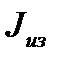 А
А
| 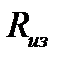 Ом
Ом
| 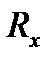 Ом
Ом
| 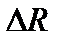
|  % %
| 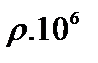 Ом . м
Ом . м
|
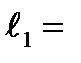
| ||||||||
| Среднее значение | ||||||||
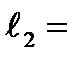
| ||||||||
| Среднее значение | ||||||||
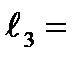
| ||||||||
| Среднее значение | ||||||||
Среднее значение 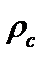
|
Таблица 4.1.2
| Номер задания | ||||||||
| Величина | 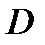
| 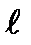
| 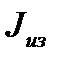
| 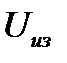
| 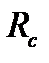
| 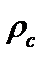
| 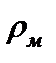
| 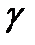
|
| Наименование единицы измерения | ||||||||
| Численное значение |
Таблица 4.1.2 (окончание)
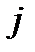
| 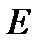
| 
| 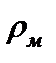
| 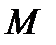
| 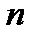
| 
| 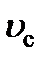
| 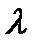
| 
|
4.2. Упражнение 2. Исследование зависимости
Дата добавления: 2015-08-18; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сопротивления проводника на основе закона Ома | | | Теория метода |