Теория метода. Проверка зависимости углового ускорения от момента инерции маятника

Проверка зависимости углового ускорения от момента инерции маятника. Для проверки обратно-пропорциональной зависимости углового ускорения от момента

инерции маятника при постоянном моменте силы 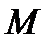(2.3) момент инерции маятника 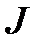изменяют, закрепляя цилиндрические грузы 5 на стержнях 1 на разных расстояниях от оси вращения.

Значения момента инерции маятника при разных положениях грузов 5 на стержнях находим по основному закону динамики вращательного движения

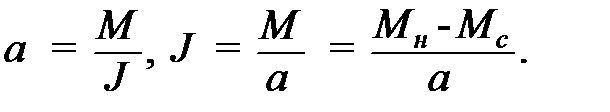
Для этого при одном и том же шкиве 3 или 4, при одном и том же грузе 8 и при одной и той же высоте падения груза 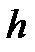, но при различных расстояниях , измеряют время падения груза 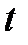и вычисляют угловые ускорения (см. задание 3,г к упражнению 1) и момент силы 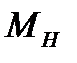(см. задание 6 к упражнению 1) при различных .

Расчеты показывают, что момент силы 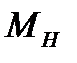от и 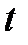зависит слабо. Поэтому, принимая за 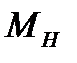среднее значение, можно допустить, что

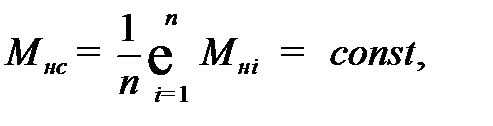
где 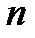– число выбранных расстояний (число вычисленных значений ).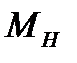

Пренебрегая зависимостью момента сил сопротивления 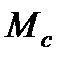от скорости вращения маятника, можно принять

= = .

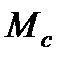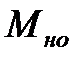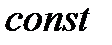Тогда

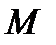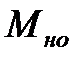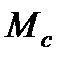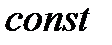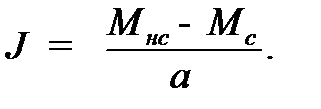= – = ; (2.7)

Вычислив 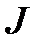и при различных и 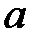и построив график зависимости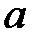

от 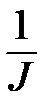, убеждаемся, что 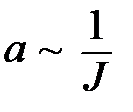, т.е. угловое ускорение действительно обратно пропорционально моменту инерции маятника.

Проверка зависимости момента инерции тела от расстояния до оси вращения (проверка теоремы Штейнера). Момент инерции системы тел равен сумме моментов инерции тел, составляющих систему тел. Поэтому момент инерции маятника 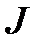складывается из момента инерции крестовины (без грузов на стержнях) 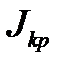и момента инерции цилиндрических грузов 5 на стержнях :

= + .

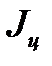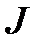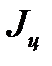Если грузы закреплены на одинаковых расстояниях от оси крестовины (оси вращения), то моменты инерции 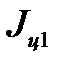грузов 5 одинаковы. Тогда

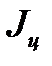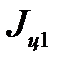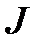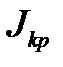= 4 ; = + 4 .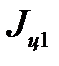

По теореме Штейнера момент инерции каждого груза 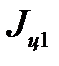равен сумме момента инерции груза 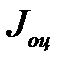относительно оси, проходящей через центр инерции груза (через середину груза) перпендикулярно оси груза, и произведения массы груза 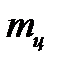на квадрат расстояния 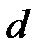от оси вращения до центра инерции груза:

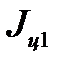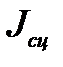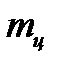
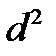= + . (2.8)

Рассматривая груз как стержень, по таблице формул момента инерции находим

= ,

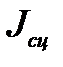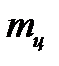
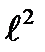где 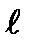– длина груза (высота цилиндрического груза).

Тогда

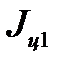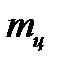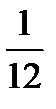
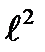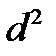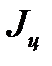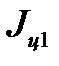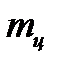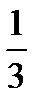
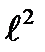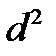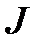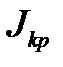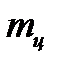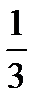
= ( + ); = 4 = ( 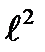+ 4 );

= + ( + 4 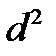). (2.9)

Таким образом, проверка формулы теоремы Штейнера для одного груза (2.8) сводится к проверке линейной зависимости момента инерции маятника 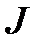от 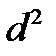(2.9). Используя значения 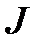, вычисленные по формуле (2.7) и построив график зависимости 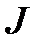от 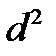, можно убедиться в линейной зависимости 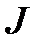от 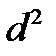, т.е. в справедливости теоремы Штейнера.

Определение момента инерции крестовины. График линейной зависимости момента инерции маятника 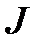от квадрата расстояния грузов до оси вращения 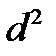позволяет определить момент инерции крестовины .

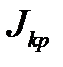Отрезок 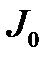, отсекаемый графиком на оси 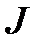, соответствует расстоянию 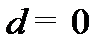м и равен моменту инерции маятника, если бы центры грузов находились на оси вращения. Согласно (2.9) при 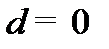м

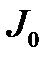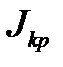= + 4 = + .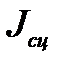

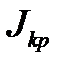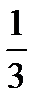
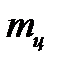
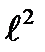Отсюда

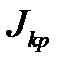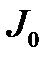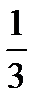
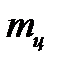
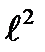= - . (2.10)

Определив 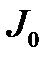по графику, используя заданные значения 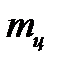и 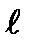, можно найти момент инерции крестовины .

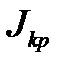Дата добавления: 2015-08-18