
|
Читайте также: |
(результаты вычислений внести в таблицы 2.2.1, 2.2.2, 2.2.3)
1) Вычислить массы грузов 8.
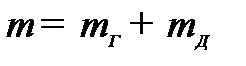
2) Вычислить среднее значение времени падения груза при всех массах груза 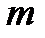 и диаметрах шкивов
и диаметрах шкивов 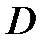 :
:

3) Учитывая, что падение груза и вращение маятника равноускоренное, выразить через высоту падения 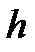 и время падения груза
и время падения груза 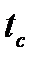 и вычислить при одном из значений величин
и вычислить при одном из значений величин 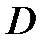 ,
, 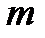 ,
, 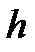 ,
, 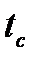 :
:
а) ускорение падения груза 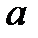 , используя формулу пути при равноускоренном прямолинейном движении;
, используя формулу пути при равноускоренном прямолинейном движении;
б) скорость груза в конце падения 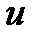 , используя формулу скорости при равноускоренном прямолинейном движении;
, используя формулу скорости при равноускоренном прямолинейном движении;
в) угловую скорость вращения маятника 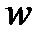 , используя связь
, используя связь 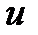 с
с  и принимая, что нить намотана на шкив плотно и проскальзывания нити по шкиву нет и линейная скорость точек цилиндрической поверхности обода шкива
и принимая, что нить намотана на шкив плотно и проскальзывания нити по шкиву нет и линейная скорость точек цилиндрической поверхности обода шкива 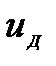 равна скорости движения груза
равна скорости движения груза 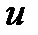 ;
;
г) угловое ускорение маятника 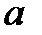 при падении груза, используя связь
при падении груза, используя связь 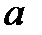 с тангенциальным ускорением
с тангенциальным ускорением 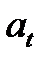 и предполагая, что проскальзывание нити по шкиву и
и предполагая, что проскальзывание нити по шкиву и
растяжение нити отсутствуют и тангенциальное ускорение точек обода шкива 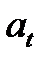 равно ускорению падения груза
равно ускорению падения груза 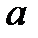 ;
;
д) угол поворота маятника 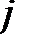 за время падения груза;
за время падения груза;
е) число оборотов маятника 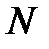 за время падения груза.
за время падения груза.
4) Используя формулу второго закона Ньютона, пренебрегая массой нити и действующими на груз силой сопротивления воздуха и силой Архимеда, получить выражение силы натяжения нити 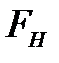 через измеренные величины
через измеренные величины 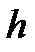 и
и 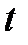 и заданную массу груза
и заданную массу груза 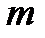 :
:
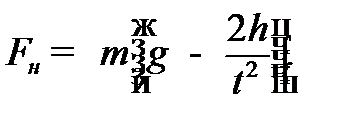
5) Вычислить силу натяжения 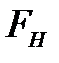 для выбранных в задании 3 значений
для выбранных в задании 3 значений 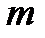 ,
, 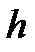 ,
, 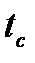 .
.
6) Пренебрегая массой нити и массой блока 7 и силой сопротивления, действующей на блок, принимая, что нить действует на шкив с силой, по величине равной 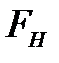 , и, используя выражение момента силы через плечо силы, получить выражение момента силы натяжения
, и, используя выражение момента силы через плечо силы, получить выражение момента силы натяжения 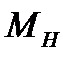 через
через 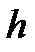 ,
, 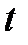 ,
, 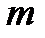 ,
, 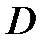 :
:
7) Вычислить момент силы натяжения 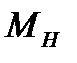 и угловое ускорение
и угловое ускорение 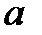 (см. задание 3,г) при всех
(см. задание 3,г) при всех 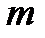 ,
, 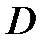 ,
, 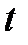 .
.
8) Построить график зависимости углового ускорения 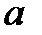 от момента силы натяжения
от момента силы натяжения 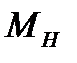 и убедиться в линейной зависимости
и убедиться в линейной зависимости 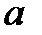 от
от 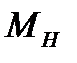 и прямо-пропорциональной зависимости
и прямо-пропорциональной зависимости 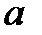 от алгебраической суммы момента силы
от алгебраической суммы момента силы 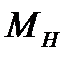 и момента силы сопротивления:
и момента силы сопротивления: 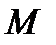 =
= 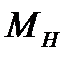 -
- 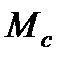 :
:
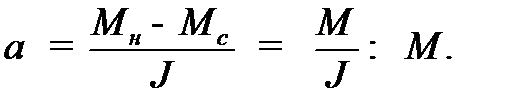
9) Выбрав интервал значений момента сил натяжения 
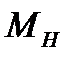 , по графику найти соответствующий интервал значений углового ускорения
, по графику найти соответствующий интервал значений углового ускорения 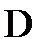
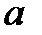 .
.
10) Учитывая, что тангенс угла наклона графика зависимости 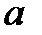 от
от 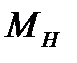
равен 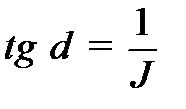 и
и 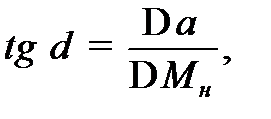 вычислить момент инерции маятника
вычислить момент инерции маятника 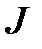 при
при
выбранном расположении грузов 5 на стержнях.
11) Обозначив момент силы 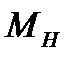 при
при 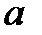 = 0 через
= 0 через 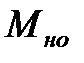 и определив
и определив 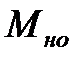 по графику, найти значение момента силы сопротивления
по графику, найти значение момента силы сопротивления
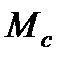 =
= 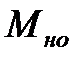 .
.
12) Принимая за нулевой уровень потенциальной энергии груза поверхность столика установки, выразить через массу m груза 8, высоту 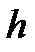 и время
и время 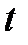 падения груза, диаметр шкива D и вычислить для выбранных значений
падения груза, диаметр шкива D и вычислить для выбранных значений 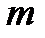 ,
, 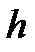 ,
, 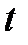 ,
, 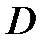 :
:
а) механическую энергию груза 8 в начале падения 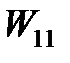 ;
;
б) механическую энергию маятника в начале падения груза 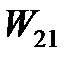 , принимая за нулевой уровень потенциальной энергии маятника горизонтальную плоскость крестовины;
, принимая за нулевой уровень потенциальной энергии маятника горизонтальную плоскость крестовины;
в) механическую энергию системы, состоящей из груза и маятника, в начале падения груза 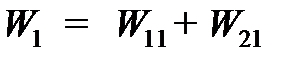 .
.
г) кинетическую энергию поступательного движения груза 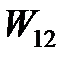 в конце падения;
в конце падения;
д) кинетическую энергию вращательного движения маятника 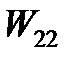 в конце падения груза;
в конце падения груза;
е) механическую энергию системы 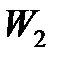 , состоящей из груза и маятника в конце падения груза;
, состоящей из груза и маятника в конце падения груза;
ж) изменение механической энергии системы 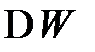 при падении груза;
при падении груза;
з) работу неконсервативных сил сопротивления при падении груза 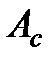 ;
;
и) работу момента сил сопротивления, действующих на маятник, при падении груза 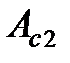
к) работу сил сопротивления, действующих на груз при его падении: 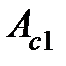 =
= 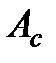 –
– 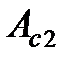 .
.
13) Используя формулу, выражающую определение работы силы, найти силу сопротивления, действующую на груз при его падении.
Таблица 2.2.1
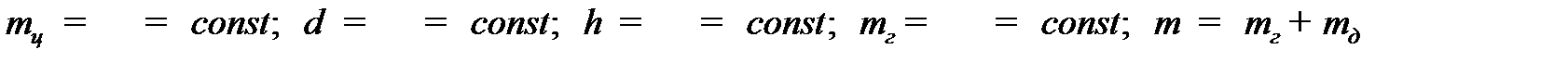
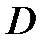 ,
м ,
м
| 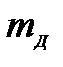 ,
кг ,
кг
| 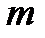 ,
кг ,
кг
| 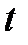 , с , с
| 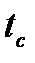 ,
с ,
с
| 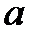 ,
с-2 ,
с-2
| 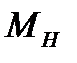 ,
Н м ,
Н м
| |||
Таблица 2.2.2
| Номер задания | 3,а | 3,б | 3,в | 3,г | 3,д | 3,е | |||||||||
| Величина | 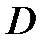
| 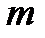
| 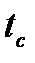
| 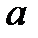
| 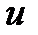
| 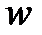
| 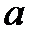
| 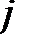
| 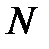
| 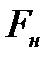
| 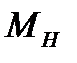
| 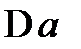
| 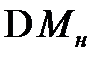
| 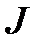
| 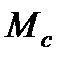
|
| Наименование единицы измерения | |||||||||||||||
| Численное значение |
Таблица 2.2.3
| Номер задания | 12,а | 12,б | 12,в | 12,г | 12,д | 12,е | 12,ж | 12,з | 12,и | 12,к | |||||
| Величина | 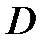
| 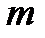
| 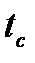
| 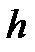
| 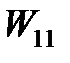
| 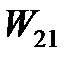
| 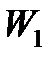
| 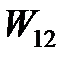
| 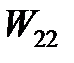
| 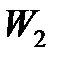
| 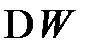
| 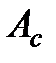
| 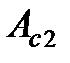
| 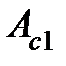
| 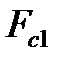
|
| Наимено-вание единицы измерения | |||||||||||||||
| Численное значение |
2.3. Упражнение 2. Проверка зависимости углового ускорения
от момента инерции маятникаи зависимости момента инерции тела от расстояния до оси вращения (теоремы Штейнера)
Дата добавления: 2015-08-18; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Порядок выполнения упражнения 1 | | | Теория метода |