
Читайте также:
|
Замкнутую систему рассматриваемого ЭП с ОС по скольжению для режима стабилизации скорости при релейном, в функции выпрямленного тока, управлении коммутатором, без учёта дискретности его работы при среднем значении импульсно-регулируемого сопротивления можно представить следующей системой уравнений [3]:
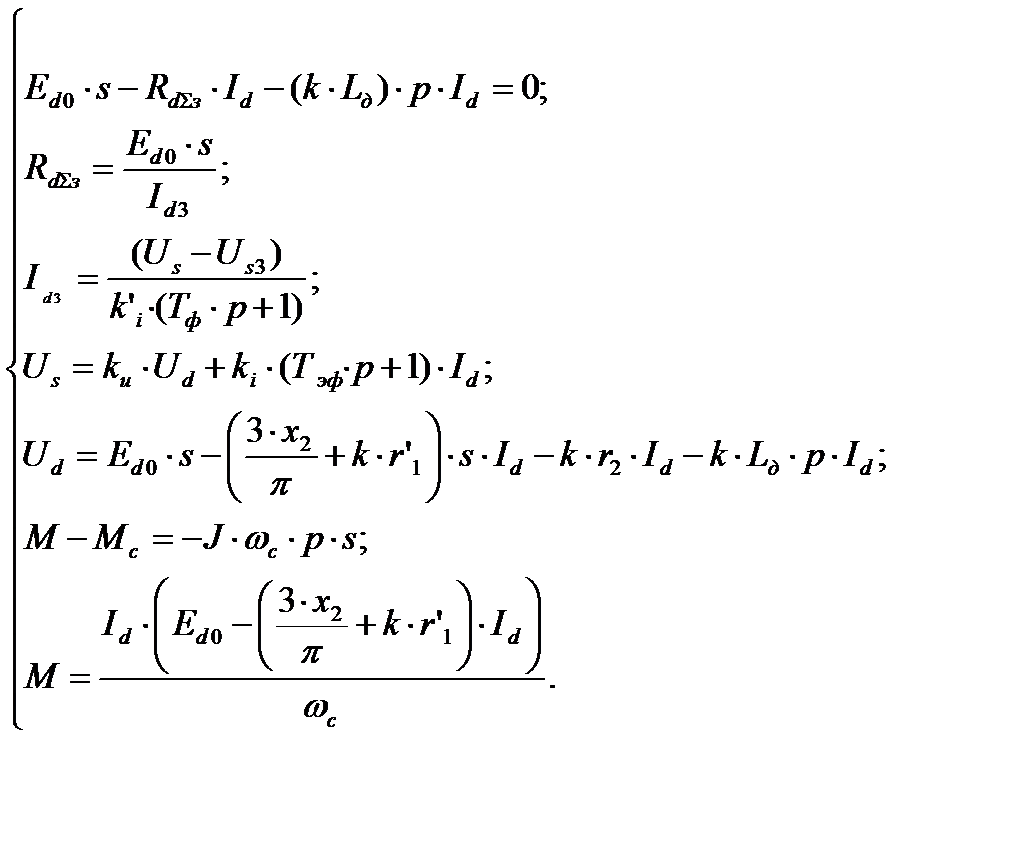
Этой системе уравнений соответствует структурная схема, представленная на рис. 3.1.
На ней видно, что система содержит нелинейности и чтобы иметь возможность исследовать электропривод линейными методами, проведем линеаризацию этих уравнений относительно точки механической характеристики с координатами (Мст; ωст1; Sст1; Iст) [3].

Рис.3.1. Структурная схема ЭП с ОС по скольжению без учёта дискретности работы коммутатора.
Линеаризованная система уравнений для точки разложения с координатами (Мст(Iст); ωст1(sст1)) имеет вид:
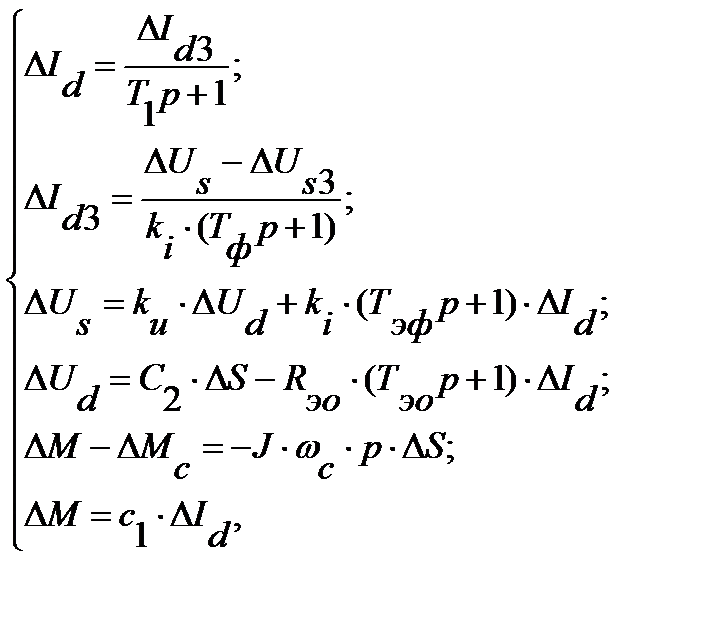

где  ;
;  ;
;  ;
;
Rэо и Тэо – эквивалентное сопротивление и электромагнитная постоянная в точке линеаризации.
При преобразовании структурной схемы линеаризованной системы можно получить передаточную функцию разомкнутой системы по управляющему воздействию:
 .
.
Структурная схема линеаризованной системы электропривода представлена на рис.3.2.

Рис.3.2. Линеаризованная структурная схема ЭП.
Выражения для вещественной и мнимой частей соответствует амплитудно-фазовой характеристики:
 ;
;  ,
,
где 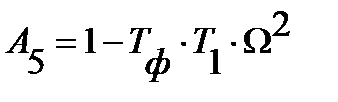 ;
;  ;
; 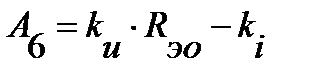 ;
;
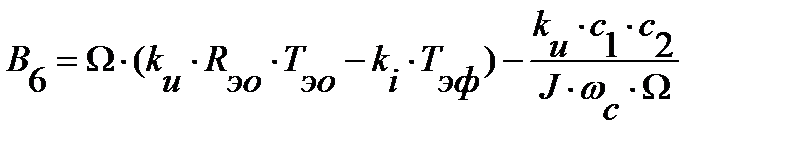 .
.
Передаточная функция разомкнутой системы по возмущающему воздействию:
 .
.
Соответствующие выражения для Р и Q:
 ;
;
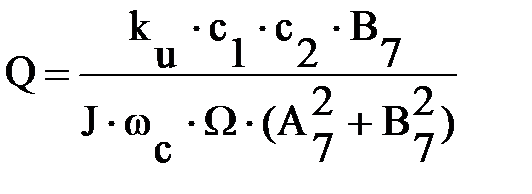 .
.
По найденным значениям Р и Q рассчитываются амплитудно-частотная и фазо-частотная характеристики в соответствии с формулами:
 ;
;
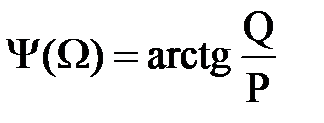 .
.
Дата добавления: 2015-08-18; просмотров: 141 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Синтез системы автоматического регулирования | | | Анализ динамических свойств системы частотным методом |