Условная переходная функция распределения

Определим функцию распределения времени пребывания процесса в -состоянии при условии, что выход из -состояния обусловлен переходом, возникающим в -ом парциальном потоке .

Пусть вектор 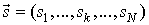фиксирует некоторое состояние процесса . Вектор 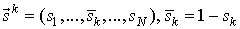задает состояние, смежное с -состоянием по -ой компоненте. Тогда индексы означают переход из -состояния в состояние .

Обозначим 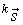вектор, не содержащий -ой компоненты, т.е. .

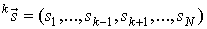Пусть 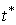- случайный момент времени, равномерно распределенный на полуинтервале .

Введем случайные величины:

- длина интервала, отсчитанного от точки 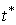до ближайшего справа скачка в потоке (недоскок процесса );

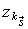- длина интервала, отсчитанного от 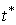до ближайшего справа скачка суперпозиции потоков 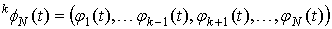или недоскок указанного процесса;

- недоскок процесса при условии перехода из состояния в состояние .

В соответствии с формулой Пальма запишем выражения для плотностей распределения вероятностей введенных величин:

- плотность распределения недоскока :

(12)

.

- плотность распределения недоскока :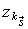

(13)

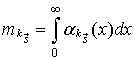
где - плотность распределения времени пребывания процесса в состоянии ;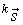

- плотность распределения недоскока :

(14)

где - плотность распределения времени пребывания процесса в -состоянии, при условии последующего перехода в смежное состояние .

Определим вероятность одновременного выполнения неравенств:

.

Вследствие независимости величин 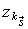и получим

(15)

Здесь

- одношаговая вероятность перехода из состояния в состояние .

После дифференцирования обеих частей уравнения (15) с учетом выражения (12) получим

. (16)

Здесь

Из условий (2) и (3) следует, что Поэтому

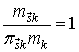
Тогда формулу (16) можно переписать в следующем виде:

, (17)

где

.

Найдем функцию распределения :

Обозначив , получим

Плотность распределения времени пребывания процесса в состоянии 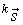равна плотности распределения длительности импульсов потока совпадения, заданного вектором 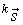. Согласно соотношению (11) плотность равна:

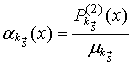(18)

Здесь

Тогда и

(19)

Следовательно

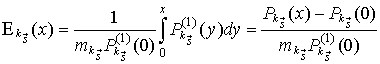. (20)

Математическое ожидание 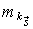времени пребывания процесса в 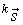-состоянии равно средней длительности импульса совпадения, которую можно найти по формуле (9) при :

Подставив выражение для в формулу (20), получим:

(21)

Выразим функцию распределения через вероятность , определяемую выражением (4). Для этого по аналогии с (18) запишем

Тогда

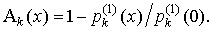(22)

Подставив выражения (21) и (22) в (17) получим формулу для искомой условной переходной функции распределения

(23)

Обозначим

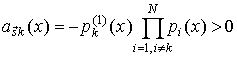(24)

Учитывая, что , получим

(25)

и окончательно

(23а)

Дата добавления: 2015-08-18