Постановка задачи. Условия и ограничения

Рассмотрим систему, состоящую из 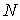элементов, каждый из которых может находиться в одном из двух состояний {0; 1}. Пусть состояния 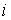-го элемента описывается случайным потоком прямоугольных импульсов .

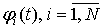Представим суперпозицию потоков 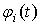вектором, компонентами которого являются парциальные потоки :

,

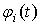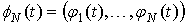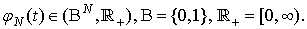
Процесс 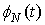находится в момент 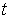в 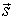-состоянии, если 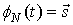, 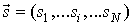. Во времени эти состояния описываются потоком 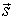-состояний

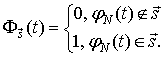
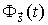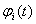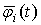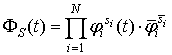Поток может быть представлен произведением соответствующих комбинаций парциальных потоков и их инверсий [1]:

(1)

где .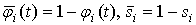

Соотношение (1) справедливо для любых типов парциальных потоков, в том числе и зависимых. Однако в настоящей работе введены ограничения на свойства потоков 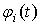, а именно полагаем что:

1) потоки стационарны, т.е. законы распределения длительностей импульсов 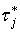и пауз 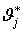не зависят от ;

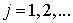2) существуют и заданы плотности распределения вероятностей длительностей импульсов 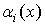и длительностей пауз ;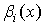

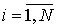3) импульсы, принадлежащие одному и тому же потоку, не перекрываются сами с собой, т.е. функция распределения длительности пауз 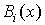не имеет скачка при :

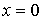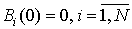(2)

4) аналогичному условию удовлетворяет функция распределения 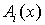длительности импульсов:

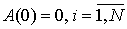(3)

5) существуют математические ожидания длительностей импульсов 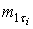и пауз ;

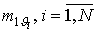6) потоки 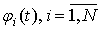взаимно независимы в совокупности.

Каждому состоянию 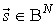можно приписать некоторое значение 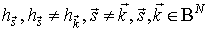. Тогда многомерному потоку 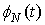соответствует процесс 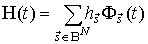, имеющий, например, смысл эффективности функционирования системы.

Процессы 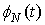и 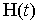относятся к классу полумарковских. Действительно, переходы из фазовых состояний описываются эргодической цепью Маркова, поскольку интуитивно ясно^[1], что цепь возвратна и средние времена возвращений конечны [2], а распределения времени пребывания системы в фиксированном состоянии в общем случае отличается от экспоненциального.

Полумарковский процесс задан, если известны вероятности переходов и условные распределения длительности пребывания процесса в фиксированном состоянии.

Настоящая работа посвящена определению этих характеристик для процессов, описываемых суперпозицией 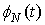случайных потоков прямоугольных импульсов.

Дата добавления: 2015-08-18