
|
Читайте также: |
№1.

Высота цилиндра 6см, радиус основания 5см.
Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.
Дано: Н = 6см, R = 5см, ОЕ = 4см.
Найти: Sсеч.
Решение:
Sсеч.= КМ×КС,
ОЕ = 4 см, КС = 6 см.
Треугольник ОКМ − равнобедренный (ОК =ОМ = R= 5см),
треугольник ОЕК − прямоугольный.
Из треугольника ОЕК, по теореме Пифагора: ЕК =3
КМ = 2ЕК = 2×3 = 6,
Sсеч.= 6×6 = 36 см2.
Ответ: Sсеч.= 36 см2
№2.
Объём первого цилиндра равен 12 куб. м. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объём второго цилиндра. Ответ дайте в кубических метрах.
Решение:
Пусть объём первого цилиндра равен: 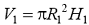
объём второго:

R1,2 – радиусы оснований цилиндров;
H1,2 – высоты;
По условию:


Выразим объём второго цилиндра через объём первого:

— Ответ: 9 куб.м.
№3. Осевым сечением цилиндра является квадрат, диагональ которого равна 6 см. 
Найдите площадь поверхности цилиндра.
Дано: цилиндр,
АВСD -осевое сечение,
АВ = АD, ВD 6= см.
Найти: Sпов.цил
Решение:
Из прямоугольного треугольника АВD по теореме Пифагора:  =2*
=2*  , откуда сторона квадрата АВ=4(см). Поэтому высота цилиндра АВ = 4 см, радиус цилиндра ОА =2 см.
, откуда сторона квадрата АВ=4(см). Поэтому высота цилиндра АВ = 4 см, радиус цилиндра ОА =2 см.
Площадь боковой поверхности Sбок.ц = 2*  h = 2*2*4 *
h = 2*2*4 * 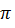 = 16
= 16  (см2).
(см2).
Площадь основания Sосн. = 2 *  = 2*4 = 8
= 2*4 = 8  (см2).
(см2).
Площадь полной поверхности Sпов.цил. = Sбок.ц + Sосн. = 16  + 8
+ 8  = 24
= 24  (см2).
(см2).
— Ответ: 24  (см2).
(см2).
№4.
Дано:  , h=10 cм
, h=10 cм

Периметр осевого сечения цилиндра равен 32 см. Найдите площадь боковой поверхности цилиндра, если его высота равна 10 см.
— Решение:
Осевое сечение цилиндра – это прямоугольник, 2 стороны которого – высоты цилиндра, в две другие – его диаметры. Т.к. его периметр равен 32 см, а высота цилиндра составляет 10 см:
 ,
,
то диаметр цилиндра равен 6 см.
Боковая поверхность цилиндра вычисляется, как произведение длины окружности основания на высоту и составит

Ответ: 
Дата добавления: 2015-08-17; просмотров: 361 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Площадь поверхности. | | | Применение. |