Теоретическое введение

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

Ивановский государственный энергетический университет

имени В.И. Ленина»

Кафедра теоретических основ теплотехники

Расчётно-графическая работа по ТМО в ЯЭУ

Вариант №7

Цилиндр

Выполнил: студент гр. 3-11^х

Н.М. Попов

Принял: доцент

Ю.С. Солнышкова

Оценка ___________

Иваново 2014

Теоретическое введение

Дифференциальное уравнение теплопроводности в векторной форме:

.

При стационарном процессе теплопроводности температурное поле не изменяется во времени, следовательно, и дифференциальное уравнение Фурье принимает вид:

.

При допущении 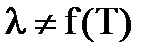, дифференциальное уравнение теплопроводности упрощается:

.

Раскрывая значение для тел простейшей (классической) формы получаем:

;

или в дивергентной форме

.

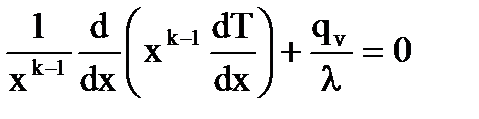Теплопроводность неограниченного однородного цилиндрического стержня

Температурное поле при охлаждении неограниченного цилиндра с внутренними источниками теплоты изображено на рис. 2.

R  

R  

r  

-r  

T, °C    

T_w  

T_w  

T_f  

T_f  

T_c  

a  

a  

Q

Q

Рис. 1. Температурное поле в неограниченном цилиндре при действии равномерно распределенных внутренних источников теплоты

Для определения температурного поля и теплового потока в цилиндре необходимо задать геометрию расчетной области (коэффициент формы тела k = 2 и размер расчетной области R=D/2, где D – диаметр цилиндра), коэффициент теплопроводности материала цилиндра l, мощность внутренних источников теплоты q_v, температуру теплоносителя T_f и коэффициент теплоотдачи a от поверхности цилиндра к текучей среде. Краткая форма записи исходных и искомых величин имеет вид:

Дано:k = 2; ; l; q_v; a; T_f;

Найти: T(r); T_c; T_w; DT; Q(r); q _l

где r_ц – радиус цилиндра; T_c и T_w – температура оси и поверхности цилиндра; DT – перепад температур по сечению цилиндра; q _l – линейная плотность теплового потока.

Математическая формулировка задачи

Дифференциальное уравнение теплопроводности:

;

или в дивергентной форме

(1)

Граничные условия:

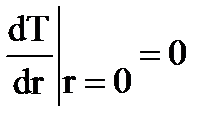; (2)

. (3)

Метод решения

Метод решения – аналитический метод разделения переменных. Предварительно умножим на «r» все члены дифференциального уравнения (II.1), записанного в дивергентной форме. Получим:

. (4)

Разделяем переменные и интегрируем первый раз:

.

Получаем:

. (5)

Делим на «r» все члены дифференциального уравнения (II.5):

или

. (6)

Разделяем переменные и, интегрируя второй раз, находим общий интеграл дифференциального уравнения теплопроводности (II.1):

;

(7)

Находим постоянные интегрирования С₁ и С₂. Для этого применим граничные условия (II.2) и (II.3). Из граничного условия на оси цилиндра и выражения (II.5) следует, что С₁ = 0. Тогда общее решение (II.7) примет вид:

. (8)

Из последнего выражения, записанного для поверхности цилиндра ( и ) имеем:

. (9)

Подставляя С₂ в общий интеграл (II.8), получаем решение дифференциального уравнения теплопроводности (II.1) при граничных условиях I рода:

. (10)

Из уравнения граничных условий III рода (II.3) выразим температуру на внешней границе цилиндра. Получим:

. (11)

Значение производной температуры на поверхности цилиндра () найдем из выражения (II.6) с учетом С₁ = 0:

. (12)

Подставляя (II.12) в (II.11), находим температуру на поверхности цилиндра:

. (13)

И, подставляя выражение (II.13) в формулу (II.10), окончательно получим решение дифференциального уравнения теплопроводности (II.1) при граничных условиях третьего рода:

(14)

Из уравнения (II.14) видно, что температура по сечению цилиндра изменяется по закону параболы. Температуру в тепловом центре 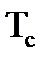цилиндра рассчитывают по формуле, полученной из выражения (II.14) при r = 0:

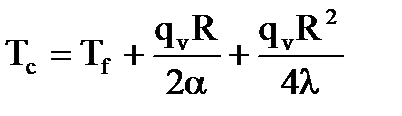(15)

Перепад температур по сечению цилиндра равен:

(16)

Тепловой поток найдем, используя закон Фурье и уравнение температурного поля (II.14):

. (17)

Тепловой поток, уходящий с поверхности цилиндра равен:

, (18)

где V – объем, м³; – длина (высота) цилиндра, м.

Линейная плотность теплового потока на поверхности цилиндра равна:

. (19)

Плотность теплового потока на поверхности цилиндра равна:

. (20)

Температурное поле цилиндра при граничных условиях

I рода

Теплообмен при граничных условиях первого рода является частным случаем теплообмена при граничных условиях третьего рода. Пр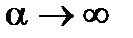и и получаем:

. (21)

. (22)

. (23)

Дата добавления: 2015-08-17