Парный регрессионный анализ

Роль математического моделирования в экономике.

Существует значительное разнообразие видов, типов экономико-математических моделей, необходимых для использования в управлении экономическими объектами и процессами.

Экономико-математические модели подразделяются на макроэкономические и микроэкономические в зависимости от уровня моделируемого объекта управления, динамические, которые характеризуют изменения объекта управления во времени, и статические, которые описывают взаимосвязи между разными параметрами, показателями объекта именно в то время.

Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени.

Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в моделях, выделяются экономико-статистические, модели линейного и нелинейного программирования, матричные модели, сетевые модели.

Факторные модели. В группу экономико-математических факторных моделей входят модели, которые с одной стороны включают экономические факторы, от которых зависит состояние управляемого экономического объекта, а с другой - зависимые от этих факторов параметры состояния объекта. Если факторы известны, то модель позволяет определить искомые параметры. Факторные модели чаще всего предоставлены простыми в математическом отношении линейными или статическими функциями, которые характеризуют связь между факторами и зависимыми от них параметрами экономического объекта.

Балансовые модели. Балансовые модели как статистические, так и динамические широко применяются в экономико-математическом моделировании. В основе создания этих моделей лежит балансовый метод - метод взаимного сопоставления материальных, трудовых и финансовых ресурсов и потребностей в них. Описывая экономическую систему в целом, под её балансовой моделью понимают систему уравнений, каждое из которых выражает потребность баланса между изготовленными отдельными экономическими объектами количества продукции и совокупной потребностью в этой продукции. При таком подходе экономическая система состоит из экономических объектов, каждый из которых выпускает некоторый продукт. Если вместо понятия «продукт» ввести понятие «ресурс», то под балансовой моделью необходимо понимать систему уравнений, которые удовлетворяют требования между определенным ресурсом и его использованием.

Наиболее важные виды балансовых моделей:

· Материальные, трудовые и финансовые балансы для экономики в целом и отдельных ее отраслей;

· Межотраслевые балансы;

· Матричные балансы предприятий и фирм.

Оптимизационные модели. Большой класс экономико-математических моделей образуют оптимизационные модели, которые позволяют выбрать из всех решений наилучший оптимальный вариант. В математическом содержании оптимальность понимается как достижение экстремума критерия оптимальности, называемой также целевой функцией. Оптимизационные модели чаще всего используются в задачах нахождения лучшего способа использования экономических ресурсов, что позволяет достичь максимального целевого эффекта.

4. Системный подход к процессу моделирования. Сист-й подход-методология исслед-я объекта и постоения его мат.модели,когда объект рассм-ся как целост-й комплекс взаимод-х комп-в, имеющ-х особое ед-во с внеш.средой и предст-т собой подсистему сист-ы более высокого порядка.При моделир-ии систем необ-мо учитывать:*целост -ть (устой-ое отнош-е м/у элемен-ми сист-ы, при этом сост-е любого элемента зависит от сост-я всей сист-ы и наоборот),* делимость (целост-й объект м.б. изображен как расчлен-й на элем-ты),* изолиров-ть (комплекс объектов, образ-х сист-у и связи м/у ними можно выделить из их окружения и рассм-ть изолир-ия),* устойч-ть (сист-а должна норм.функц-ть и быть не чувств-й к неизб-м возмущ-м воздейств-м),* разнообразие (кажд.элемент сист-ы обладает собствен-м повед-м и сост-м, отлич-м от поведения и сост-я др. элем-ов и сист-ы в целом),* идентиф-ть (кажд.элемент сист-ы м.б. отделен),* стабил-ия (сист-а осущ-т восст-ие своих элем-ов за счет их регулир-ия),* наблюд-ть (все без искл-я входы и выходы сист-ы либо контролир-ы исследо-м, либо наблюдаемы),* неопред-ть (ислед-ль одновремен-о не может фиксир-ть все свой-ва и отнош-я элемен-в сист-ы),* нетождест-ть (отображ-ся знаковая сист-а исслед-ля,отличная от знак.сист-ы прояв-ля свой-в объектов и их отношений),* адаптация (сист-а сохр-ет сост-е подвиж-го равнов-я и устой-ть к возмущ-ым воздей-м,к-м она пост-но подверг-ся путем перестройки внутр.струк-ры и функц-й отдель.элемен-в.

5. Основные элементы моделирования. Метод моделир-я вкл. 3 элемен-та:* субъект (исслед-ль),* объект исслед-я,* модель, опосред-го отношения познающего субъект и познав-го объекта. Процесс постр-ия моделей осущ-ся в неск-ко этапов(постановка задачи, опреде-е задачи,сост-е матем-й модели, вычисление, выдача резуль-в). Выбор объектов модел-ия происходит на 2м этапе - определение задачи.Здесь исслед-ль старается опред-ть к какому виду относ-ся объект,описыв-т параметры сост-я объекта, перем-ые харак-ки, факторы внеш.среды.Необх-мо понять законом-ти внутр.организ-ии объекта, постр-ть модели струк-ры.Эта работа наз-ся идентиф-ей сист-ы - выявление и изучение сист-ы.

6. Этапы построения математических моделей. Обычно процесс постр-ия моделей осущ-ся в неск-ко этапов(постановка задачи, опреде-е задачи,сост-е матем-й модели, вычисление, выдача резуль-в).* Постановка задачи (этапу предщест-т возник-е каких-либо проблем,осозн-е к-х приводит к мысли их обобщ-я или реш-ия для послед-го достиж-я какого-либо эффекта)* Опред-ие задачи (исслед-ль старается опред-ть к какому виду относ-ся объект,описыв-т параметры сост-я объекта, перем-ые харак-ки, факторы внеш.среды. Необходимо понять законом-ти внутр.организ-ии объекта, постр-ть модели структуры.Эта работа наз-ся идентиф-ей сист-ы-выяв-ие и изуч-е сист-ы, т.е. получ-е возможно более полную характ-ку сист-ы, ее повед-ия, познание объект-х закон-тей ее внутр.орган-ции,очерч-ие ее раниц, указание на вход,процесс и выход, опред-ие огран-я, постр-ие структ. и мат.модели.После идентиф-ии строится концеп-я модель сист-ы)* Сост-е мат.модели (вид мат..модели зависит от цели исслед-я, она м.б. предст-а виде мат.выраж-я, предств-го собой алгебраич. уравн-е или нерав-во,не имеющ-х разветв-я вычисл-го процесса при определ-ии кажд.перем-й сост-й сист-ы целев-й функ-ии и уравн-й связи.* вычисление (при реш-ии задач необ-мо тщат-но разобр-ся с размерн-тью всех величин,вход-х в мат.модель и опред-ть границы,в кот-х будет лежать искомая цел-я ф-я.необх-мо задат-ся точностью вычесления)* выдача резул-в (рез-ты исслед-й объекта могут выдав-ся в уст. или пись. форме, они должны вкл. в себя краткое опис-е объктов исслед-я,цели исслед-я, выьран-ю мат.модель, допущ-я и огранич-я,осн.рез-ты вычисл-й,выводы и обощ-я)

7. Принципы построения концептуальной модели. Первым этапом мат.моделир-я явл. постр-ие концепт-й модели М,сист-ы S,и ее формал-ия, т.е. осн. назн-м этого этапа явл. переход от содерж-го опис-я объекта к его мат.модели. Послед-ть постр-я концеп-й модели М, сист-ы и ее формализ-ции: постановка задачи мат.модел-ия сист-ы, анализ задачи модел-я сист-ы, опред-ие треб-й к исход-й инфор-ии об объекте модел-ия и организ-ии ее сбора,выдвиж-е гипотез и принятие предл-й,опред-ие парам-в и переем-х модели,установ-е осн.содер-ия модели,обосн-ие критер-в оценки эффект-ти сист-ы,опред-е процедур аппроксим-ции (замена одних объектов другими, в том или ином смысле близкими к исходным, но более простыми),описание конц-й модели сист-ы, проверка достоверности конц-й модели,сост-е технич.докум-ции по 1му этапу.

8. Принцип построения факторной модели объекта. Под факторным анализом поним-ся методика комплек-го и сист-го изуч-я и измер-я возд-я фактор-в на величину результ-х показа-й.В общ.случае можно выделить след-е осн.этапы постр-я факт-го анализа:постановка цели факторного анализа;отбор факторов,опред-х исслед-мые результ-ые показ-ли(осущ-ся на основе теорет.и практич. знаний в конкрет-й обл.);классиф-я и системат-я факторов с целью обеспеч-я комплек-го и сист-го подхода к исслед-ю их влияния на рез-ты хоз-й деят-ти;опред-е формы завис-ти м/у факторами и результ-м показат-м;моделир-е взаимосвз-й м/у результ-ми и фактор-ми показа-ми;расчет влияния факторов и оценка роли кажд.из них в измен-и величины результ-го показ-ля;работа с факторн.моделью(практич.использ-е ее использ-ие для управл-я эконом. процессами).

9. Корреляционно – регрессионный анализ

У = f (х₁, х₂, …, х_n) – уравнение регрессии

у – целевая функция

х – факторные независимые случайные величины

у – зависимая, но случайная величина

Известны 2 типа связей между целевой функцией и факторами:

— функциональный

— регрессионный

Регрессионная связь устанавливается с помощью уравнения регрессии, которое определяется по результатам эксперимента на основе связей между функцией и аргументами

b₁x₁ – коэффициент первого порядка

b₃x₁² – коэффициент второго порядка

b₅x₁x₂ – смешанный коэффициент первого порядка

В регрессионном анализе решаются следующие задачи:

— установление точности определения коэффициента уравнения регрессии b_i (i=0…n) в виде значения дисперсии S²/b_i или доверительных интервалов b_imin≤b_i≤b_imax

— установление значимости коэффициента b_i

— проверка адекватности установленной формы связи и экспертных данных.

Различают:

— линейный регрессионный анализ

— нелинейный регрессионный анализ

Регрессионный анализ бывает:

— однофакторный

— многофакторный

Аппарат KRA используется в двух случаях:

— для проведения статистического анализа результатов наблюдения пассивных экспериментов

совместно с методом наименьших квадратов используется при планировании статистических экспериментов и анализа результатов.

10. Метод наименьших квадратов. Суть метода наименьших квадратов. Рассмотрим содержание метода на конкретном примере. Пусть имеются данные о сборе хлеба на душу населения по совокупности черноземных губерний. От каких факторов зависит величина этого сбора? Вероятно, определяющее влияние на величину сбора хлеба оказывает величина посева и уровень урожайности. Рассмотрим сначала зависимость величины сбора хлеба на душу населения от размера посева на душу (столбцы 1 и 2)

№ п/п	у	х1	х2
	48,01	0,91	46,08
	38,18	0,76	45,18
		0,82	41,76
	46,72	0,88	50,94
	41,58	0,88	43,54

у – сбор хлеба (пуд.) на душу населения, х₁ – посев на душу (дес.), х₂ – урожай (пуд/дес)

Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.

В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемых нормальных уравнений. Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.

Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь между сбором хлеба на душу и величиной посева на душу может быть изображена с помощью прямой линии и записана в виде

где у—величина сбора хлеба на душу (результативный признак или зависимая переменная); x—величина посева на душу (факторный признак или независимая переменная); a_o и a₁ — параметры уравнения, которые могут быть найдены методом наименьших квадратов.

Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид

Полученная система может быть решена известным методом Гаусса. Искомые параметры системы из двух нормальных уравнений можно вычислить и непосредственно с помощью последовательного использования нижеприведенных формул:

где y_i — i-e значение результативного признака; x_i — i-e значение факторного признака; и — средние арифметические результативного и факторного признаков соответственно; n— число значений признака y_i, или, что то же самое, число значений признака x_i

ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

Одним из методов изучения стохастических связей между признаками является регрессионный анализ.
Регрессионный анализ представляет собой вывод уравнения регрессии, с помощью которого находится средняя величина случайной переменной (признака-результата), если величина другой (или других) переменных (признаков-факторов) известна. Он включает следующие этапы:

1. выбор формы связи (вида аналитического уравнения регрессии);

2. оценку параметров уравнения;

3. оценку качества аналитического уравнения регрессии.
Наиболее часто для описания статистической связи признаков используется линейная форма. Внимание к линейной связи объясняется четкой экономической интерпретацией ее параметров, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму.
В случае линейной парной связи уравнение регрессии примет вид: . Параметры данного уравнения а и b оцениваются по данным статистического наблюдения x и y. Результатом такой оценки является уравнение: , где , - оценки параметров a и b, 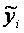- значение результативного признака (переменной), полученное по уравнению регрессии (расчетное значение).
Наиболее часто для оценки параметров используют метод наименьших квадратов (МНК).
Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (u) и независимой переменной (x).
Задача оценивания параметров линейного парного уравнения методом наименьших квадратов состоит в следующем:
получить такие оценки параметров , , при которых сумма квадратов отклонений фактических значений результативного признака - y_i от расчетных значений – 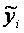минимальна.
Формально критерий МНК можно записать так:
.
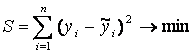Проиллюстрируем суть данного метода графически. Для этого построим точечный график по данным наблюдений (x_i,y_i, i=1;n) в прямоугольной системе координат (такой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.

Математическая запись данной задачи:
.
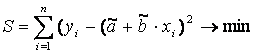Значения y_i и x_i i=1; n нам известны, это данные наблюдений. В функции S они представляют собой константы.

Дата добавления: 2015-08-17