Теорема Абеля

Теорема. Если ряд (А) сходится и имеет сумму А (в обычном смысле), то для сходится степенной ряд (1), и его сумма стремится к пределу А, когда .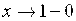

Если ряд (А) суммируем по Пуассону-Абелю к сумме А, то в обычном смысле, как мы видели, он может и не иметь суммы. Иными словами из существования предела

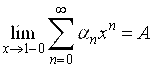, (5)

вообще говоря, не вытекает сходимость ряда (А). Естественно возникает вопрос, какие дополнительные условия надлежит наложить на поведение членов этого ряда, чтобы из (5) можно было заключить о сходимости ряда (), т.е. о существовании для него суммы в обычном смысле. Первая теорема в этом направлении была доказана Таубером.

Н.Х. Абель - знаменитый норвежский математик, который предложил одну из техник регуляризации расходящихся рядов. В ходе своей короткой жизни, он умер всего в 26 лет, Абель достиг впечатляющих результатов в решении одних из самых трудных математических задач. В частности, он показал, что решение алгебраического уравнения пятой степени не может быть найдено в радикалах, поставив тем самым точку в проблеме, которая оставалась нерешенной на протяжении 250 лет до него.

Дата добавления: 2015-08-17