Метод степенных рядов

Этот метод, по-существу принадлежит Пуассону, который сделал первую попытку применить его к тригонометрическим рядам. Он состоит в следующем.

По данному числовому ряду А= ∑a_n=a₀+a₁+…+a_n

строится степенной ряд

( 1)

Если этот ряд для сходится и его сумма при имеет предел А:

,

то число А и называют “обобщённой (в смысле Пуассона) суммой” данного ряда.

Примеры.

1) Ряд, рассмотренный Эйлером:

Здесь уже в силу самого определения приводит к степенному ряду, сумма которого при стремится к пределу . Значит, число , действительно, является “обобщенной суммой” указанного в точном установленном здесь смысле.

2) Возьмем более общий пример: тригонометрический ряд

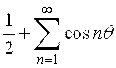(2)

является расходящимся при всех значениях

Если образовать степенной ряд:

(здесь буква заменяет прежнюю букву ), то его сумма при значении , отличном от 0, будет

(3)

и при стремится к 0. Таким образом, для “обобщенной суммой” ряда будет 0. если , то ряд (2), очевидно имеет сумму, равную ; впрочем, выражение (3), которое в этом случае сводится к , также имеет пределом .

3) Аналогично ряд

,

который сходится лишь при или , приводит к степенному ряду

.

Так что “обобщенная сумма" на этот раз оказывается равной при и равной нулю при .

Непосредственно ясно, что рассматриваемый метод “обобщенного суммирования” является линейным. Что же касается регулярности этого метода, то она устанавливается следующей теоремой Абеля.

Дата добавления: 2015-08-17