Простейшие модели.

I. Оценка темпа инфляции.

Прогноз темпа инфляции представляет собой сложную задачу, требующую учёта многих экономических, социальных, психологических и политических факторов. Такие исследования ведутся аналитическими центрами крупных финансовых и инвестиционных фирм и являются основой формирования ставок дивидендов для вкладчиков. Но по этой информации, выдаваемой фирмами, можно восстановить их оценку темпа инфляции.

Предположим, фирма обещает вкладчикам долю прибыли р_р в рублях и р_д вдолларах. Это означает, что начальный капитал в рублях а_ор через год превращается в а_1р =а_ор(1+р_р), а соответствующие величины в долларах 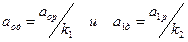(k₁, k₂ – курс доллара в начале и конце года) связаны соотношением: а_1д=а_0д (1 +р_д).

Отношение курсов доллара k₂/k₁ равно 1+γ₁=e ^γ, где γ –темп инфляции (малой инфляцией доллара можно пренебречь), и его легко выразить через р_р и р_д:

поэтому

1+γ₁=e γ = .

Очевидно, что при р_р = р_д инфляции нет, γ₁ = γ = 0. При р_р=5, р_д=0,5 (500% и 50% соответственно), γ₁ =4,5/1,5 = 3 (300%);

при р_р = 3, р_д= 0,25, γ₁ =2,75/1,25 = 2,2 (220%).

II. Оборачиваемость капитала, связанная со временем реализации.

В экономике важную роль играет оборачиваемость капитала, связанная со временем реализации продукции, произведённой (или купленной) за счёт этого капитала. Подсчитаем размеры прибыли при различной величине торговой наценки α₁ и α₂ < α₁, если увеличение наценки приводит к удвоению (для простоты расчётов) времени реализации (t₁ = 2t₂). Если годовой темп инфляции γ (e ^γ= 1+ γ₁ ), а себестоимость товара С₀, то прибыль в двух рассматриваемых вариантах равна:

если

,

т.е. получено условие, при котором увеличение наценки приводит к уменьшению прибыли.

Пусть γ =2,2; t₁ = 1/12, тогда = 0,912 и при q < 1,91 стремление к увеличению прибыли за счет увеличения торговой наценки приводит к противоположному результату.

Например, если то 0,784; следовательно, увеличение наценки в 1,5 раза, приводящее к удвоению срока реализации, дает проигрыш в прибыли (около 22%).

III. «Продажа с возвратом платежа».

Среди различных рекламных предложений можно было встретить объявления, обещающие при оплате некоторой покупки вернуть через год её стоимость и оставить приобретенный товар у покупателя. Очевидно, прибыльность такой операции для продавца опять-таки связана с неэквивалентностью затрат в разные моменты времени. Проанализируем эффективность такой «продажи с возвратом платежа».

Пусть цена продаваемого товара, приобретаемого непосредственно у производителя или со скидкой за оптовую продажу, равна Р₀, а её оплата в рамках указанной схемы Р₁ =Р₀(1+ α ).

Полученные продавцом средства инвестируются им в некоторый прибыльный процесс (производство, банк, посреднические операции) и к концу года дадут Р₂=P₁(1+р)=Р₀(1+ α )(1+р), где р – доля годовой прибыли в используемом процессе. После возврата покупателю платежа Р₁ у продавца остаётся сумма Р₀(1+ α )р, а поскольку в начале процесса он затратил Р₀, процесс этот будет определять прибыль продавца, если

Р₀(1+ α )р>Р₀ и Р₀(1+ α )р=Р₀(1+β),

где β – доля прибыли продавца в рассматриваемой операции, определяется соотношением:

1+β =(1+ α )р

Из этой формулы следуют любопытные выводы. Во-первых, легко получается условие прибыльности такой «продажи с возвратом»:

β > 0 или (1+ α )р > 1, т.е.

Следовательно при р > 1 наценка αможет быть даже отрицательной, т.е. является скидкой (!) с заводской цены, и при такой продаже со скидкой всё равно посредник имеет прибыль.

Во-вторых, запишем условие того, что эта операция оказывается выгоднее простой инвестиции средств Р₀ в используемом процессе с долей прибыли р:

β > р или (1+ α )р-1 > р т.е.

Причина такой «сверхэффективности» очевидна: в процесс «наваривания» вовлекаются большие средства (P₁>Р₀). Возможны некоторые модификации этой схемы, например, возврат покупателю не всего платежа P₁, а лишь заводской, «безналичной» цены P₀. При этом 1+β=(1+ α )(1+р)-1 =α +р+ α р, условие прибыльности принимает вид: β > 0, т.е. α> , а условие «сверхприбыльности»: β > р, т.е. α >

Или «возврат платежа с индексацией (в соответствии с темпом инфляции)», т.е. величины P₁(1+γ₁).

В последнем случае, приводя оставшуюся после возврата индексированного платежа сумму

Р₀(1+ α )(1+р) - Р₀(1+ α )(1+γ₁)

к начальному моменту времени (деля на (1+γ₁) и приравнивая Р₀(1+β)), получаем:

1+β= >0.

Соответственно, условие прибыльности (β>0) имеет вид: а условие «сверхприбыльности» (β > р):

Кроме того, дополнительная прибыль может быть получена, если за счёт льготных условий возникает более широкое привлечение капиталов покупателя, а при большем объёме инвестиций увеличивается норма прибыли р.

Очевидно также, что при малых р необходимая наценка слишком велика и эта схема нежизнеспособна (при р = 0,05 и β > р, α >1/р = 20).

IV. Вложения в образование и здравоохранение.

Отдача от работы профессионально обученного человека больше, чем от работы неподготовленного. Поэтому затраты на обучение будущих работников рассматриваются как инвестиции в человеческий капитал. Хорошее здоровье означает увеличение работоспособности, производительности труда и срока трудовой активности работников. Поэтому вложения в здравоохранение тоже можно рассматривать как инвестиции в человеческий капитал.

Рассмотрим подробно такие вложения. Предположим, что чем выше образовательный уровень, тем больше заработная плата работника. Чтобы получить высокий образовательный уровень необходимо сделать затраты (например, на обучение и компенсацию упущенных во время обучения заработков). Для правильной оценки выгодности вложений в образование необходимо дисконтирование будущих выгод и затрат.

Пусть А – затраты на обучение; С – зарплата до обучения (за год); В – ожидаемый годовой заработок после обучения; N – ожидаемый срок работы с таким заработком (в годах); α– темп отдачи вложения в обучение. Темп отдачи вложения αсоответствует темпу роста прибыли р при расчёте прироста капитала или темпу инфляции γ при оценке инфляции.

Предположим, что инфляции нет. Приведённая к начальному году ожидаемая зарплата при работе без обучения:

с обучением:

Вложение в образование выгодно, если разница в зарплате до и после обучения больше, чем затраты на обучение. Затраты на обучение складываются из упущенной зарплаты во время обучения С и стоимости обучения А. Тогда обучение выгодно, если .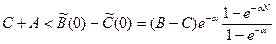

Норма отдачи вложений, как и раньше, определяется из равенства: α₁+1=е^α.

Например, пусть зарплата за год С равна 30000 руб. до обучения, годичное обучение стоит А = 15000 руб. Темп отдачи составляет 20% ( α= 0,2). Впоследствии планируется работать N=20 лет. Тогда из неравенства определим В:

30000 + 15000 <(В - 30000)

Откуда В > 40135, т.е. обучение выгодно, если после него можно претендовать на зарплату, большую чем 40135 руб. в год.

Если же планируется работать после такого обучения 3 года, то

30000 + 15000 <(В - 30000)

в этом случае В>52082, т.е. обучение целесообразно, если последующая зарплата превысит 52082 руб.

* Проценты наглядны, но в формулах часто удобно использо­вать доли.

Дата добавления: 2015-08-17