Отличие от метода касательных

Реализуя метод касательных, при каждой итерации необходимо вычислять значение не только функции 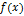, но и её производной . В методе хорд необходимо вычислять только значение .

Рассмотрим II случай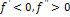

Требуется найти уравнение прямой, проходящей через две точки, , и найти координаты точки пересечения этой прямой с осью Ox.

Запишем уравнение прямой проходящей через две точки,

Выразим точку пересечения прямой AB с осью Ox.

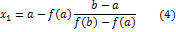
Обозначим b , тогда

Уравнение (4) определяет первое приближение через нулевую точку справа.

Аналогично строим прямую через точки . Находим точку пересечения прямой с осью Ox и выражаем через построенное уравнение. В итоге получим второе приближение. Аналогичными построениями получим приближение справа.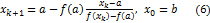

Аналогично, если взять в качестве нулевой точки точку (т.е. 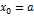), то получим соответствующее приближение слева

Для установления неподвижности точки применяется следующий критерий.

Критерий неподвижности точки:

Точка будет неподвижной тогда и только тогда, когда функция 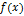и её вторая производная имеют одинаковые знаки, т.е. выполняется условие , .

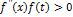Если выполняется 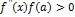, тогда выбирается левый конец отрезка 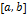(точка a) в качестве неподвижной точки и используется формула (6).

Если выполняется 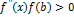, тогда выбирается правый конец отрезка 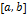(точка b) в качестве неподвижной точки и используется формула (7).

Геометрический смысл метода хорд:

Геометрический смысл метода проиллюстрирован на нижнем рисунке. В данном случае соответствует точке пересечения хорды, соединяющей концы кривой с осью абсцисс. Далее находится точка на кривой с абсциссой , проводится следующая хорда и т.д.

Условие 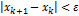является условием выхода для итерационного процесса.

Метод хорд обладает линейной сходимостью.

Погрешность стремится к нулю при .

Метод секущих

Метод секущих получается из метода касательных заменой

В результате получим формулу итерационного процесса:

где 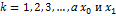должны задаваться.

Формула (8) определяет двушаговый метод (результат ()-го шага зависит от результатов k- го и - го шагов) и на каждой итерации требует вычисления только одного значения функции, другое же значение, фигурирующее в этой формуле, передаётся с предыдущего шага. Сравнив (8) с (4), полученной из геометрических соображений, легко понять, что есть абсцисса точки пересечения с осью прямой, проведённой через точки и 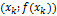, т.е. секущей (Рис. 5.9). Отсюда название этого метода - метод секущих.

Метод секущих является сверхлинейным сходящимся процессом. Можно сказать, что метод сходится двушагово квадратично.

Метод простых итераций

Заменим уравнение 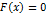равносильным уравнением

.

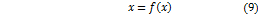Пусть 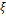- корень уравнения (9), а - полученное каким-либо способом на этапе отделения корней грубое приближение к корню 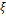. Подставляя в правую часть уравнения (9 получим некоторое число . Проделаем то же самое с , получим и т.д. Последовательно применяя рекуррентное соотношение для n = 1, 2, …, образуем итерационную последовательность (последовательность приближений):

, ,…, , … (10)

Процесс построения итерационной последовательности (10) имеет простую геометрическую интерпретацию. Последовательность приближений может быть как сходящейся,

так и расходящейся

Если последовательность сходится, а функция f - непрерывна, то предел последовательности (10) является корнем уравнения (9).

Теорема (Достаточные условия сходимости итерационного процесса)

Пусть уравнение (9) имеет единственный корень на отрезке 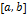и выполнены условия:

1) f - определена и дифференцируема на ;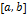

2)

3) Существует такая правильная дробь q такая, что (),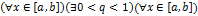

тогда итерационная последовательность (10) сходится при любом начальном члене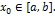

Условия теоремы не является необходимыми. Это значит, что итерационная последовательность может оказаться сходящейся и при не выполнении этих условий.

Условие выхода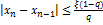

Метод простой итерации сходится, тем быстрее, чем меньше значение q.

Оценка погрешности метода

Метод простых итераций решения систем скалярных нелинейных уравнений.

Пусть требуется решить систему: (11)

заданные, вообще говоря, нелинейные вещественнозначные функции вещественных переменных , , ,тогда систему запишем в виде (11a)

F -вектор функция векторного аргумента. Таким образом решить систему (11) - значит найти нули нелинейного отображения .

Преобразуем систему (11) к виду (12) (12a)

Решить задачу (2а) - значит решить задачу о неподвижной точке нелинейного отображения .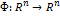

Запишем формально рекуррентное равенство:

- метод простых итераций, где .

Если начать процесс построения последовательности с некоторого нулевого приближения вектора и продолжить по (13), то при определённых условиях эта последовательность будет приближаться к т. - неподвижная точка отображения .

Теорема.

Пусть функция 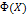и замкнутое множество таковы, что

1) ()()

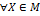2) ()()()

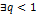Тогда имеет во множестве M единственную неподвижную точку , а последовательность (), определяемая методом простых итераций(13) при любом начальном приближении из M, т.е. 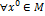сходящейся к .

При этом справедливы оценки:

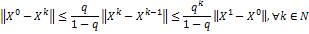
Сходимость метода простой итерации для систем нелинейных уравнений является линейной.

Условие выхода если .

Дата добавления: 2015-08-17