Вычислительная математика

Пусть имеется уравнение вида

где 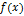- скалярная нелинейная функция.

Отделение корней.

Решить уравнение вида (1)- значит:

· Установить, имеет ли оно корни;

· Сколько корней;

· Установить наиболее «тесные» промежутки, каждый из которых содержит только один корень.

· Найти значения корней (с некоторой точностью).

Для определения наличия корней непрерывной функции 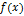воспользуемся следующей теоремой

Теорема о существовании на отрезке единственного корня непрерывной, строго монотонной функции.

Теорема (Больцано-Коши) (2).

Если непрерывная на отрезке 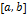функция 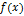на его концах имеет значения противоположных знаков, т.е. 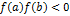, то на интервале 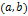она имеет хотя бы один корень.

Если, к тому же, функция монотонна, то корень единственный.

Метод половинного деления (дихотомии)

Идея метода основана на теореме Больцано-Коши

Пусть 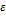- допустимая погрешность приближённого значения корня .

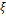Возьмём пробную точку 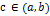, например, середину .

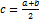Если 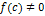(что практически наиболее вероятно), то возможны два случая: 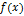меняет знак либо на интервале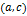 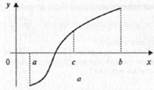либо на интервале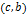

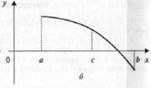
Алгоритм метода половинного деления:

Шаг 1. Вычисляем пробную точку c ();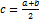

Шаг 2. Вычисляем ;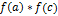

Шаг 3. Если произведение 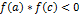(т.е. функция 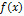меняется знак на интервале (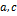)), то Шаг 4, иначе Шаг 5;

Шаг 4. Отрезок 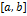заменить отрезком ;

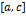Шаг 5. Отрезок 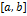заменить отрезком ;

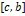Шаг 6. Если 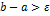, то вернуться к Шагу 1, иначе, т.е. если 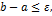прекратить вычисления и 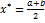(Условие выхода).

Определим скорость сходимости для итерационного процесса.

Последовательность 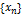, сходящаяся к пределу 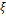, имеет порядок сходимости 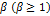, если существуют числа 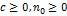, такие, что для любого 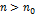выполняется неравенство .

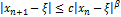Сходимость при 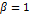называется линейной, а при 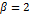- квадратичной. С увеличением 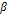вычислительный алгоритм, как правило, усложняется, а сходимость итерационной последовательности становится более быстрой.

Метод половинного деления обладает линейной сходимостью, т.к. .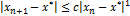

Оценка погрешности метода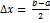

Метод касательных

Пусть 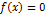имеет единственный корень на отрезке 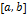. Пусть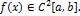

Рассмотрим 4 случая, различающихся знаком первой и второй производной функции .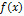

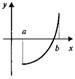
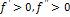- функция возрастает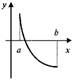 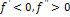- функция убывает

и вогнута (I) и вогнута (II)

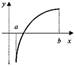
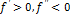- функция возрастает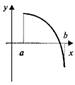 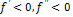- функция бывает и выпукла (III) и выпукла (IV)

Рассмотрим II случай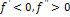

Запишем уравнение касательной к графику функции 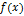в т.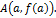

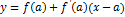
Находим точку пересечения касательной с осью Ox (ось абсцисс)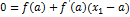

Выразим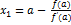

Обозначим 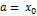, тогда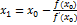

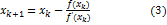где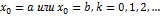

Критерий выбора точки

Через точку будет проведена касательная тогда и только тогда, когда функция 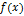и её вторая производная имеют одинаковые знаки, т.е. выполняется условие , .

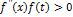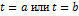Если выполняется 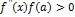, тогда выбирается левый конец отрезка 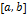(точка a) для построения касательной и используется формула (3) для 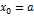(случай II и III).

Если выполняется 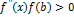, тогда выбирается правый конец отрезка 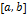(точка b) для построения касательной и используется формула (3) для 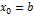(случай I и IV).

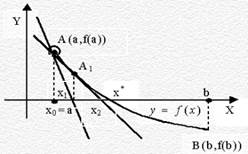
Геометрический смысл метода касательных:

Приближения к корню 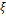совершаются по абсциссам точек пересечения касательных к графику данной функции, проводимых в точках, соответствующих предыдущим приближениям.

Условие выхода 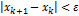или .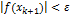

Метод касательных обладает квадратичной сходимостью, т.к. .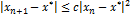

Отметим, что если начальное приближение недостаточно близко к решению, то метод может не сойтись вообще.

Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Метод хорд

Пусть 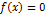имеет единственный корень на отрезке 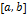. Пусть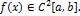

Дата добавления: 2015-08-17