Сложение взаимно перпендикулярных колебаний

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты w, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю:

(5.25)

Разность фаз обоих колебаний равна j, А и В - амплитуды складывае­мых колебаний.

Уравнение траектории результирующего колебания находится ис­ключением из выражений (5.25) параметра t. Записывая складываемые колебания в виде

и изменяя во втором уравнении coswt на х/А и sinwt на , получим после несложных преобразований уравнение эллипса, оси ко­торого ориентированы относительно координатных осей произвольно:

. (5.26)

Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз j. Рассмотрим некоторые частные случаи, представляющие физический интерес:

1. . В данном случае эллипс вырождается в отрезок прямой

, (5.27)

где знак плюс соответствует нулю и четным значениям m (рис.31, а), а знак минус - нечетным значениям m (рис. 31, б). Результирующее ко­лебание является гармоническим колебанием с частотой w и ампли­тудой , совершающимся вдоль прямой (5.27), составляющей с осью х угол . В данном случае имеем дело с линейно поляризованными колебаниями.

Рис.31

2. . В данном случае уравнение примет вид

. (5.28)

Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 32).

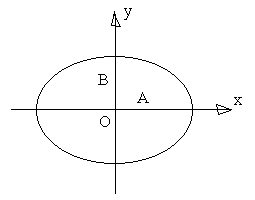Рис. 32

Кроме того, если А=В, то эллипс вы­рождается в окружность. Такие коле­бания называются циркулярно поляризованными коле­баниями или колебаниями поляризованными по кругу.

Если частоты складываемых взаимно перпендикулярных колеба­ний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, со­вершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых коле­баний. На рис. 33 представлены фигуры Лиссажу для различных соот­ношений частот (указаны слева) и разностей фаз (указаны вверху).

j=0 p/4 p/2 3p/4 p

Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу - широко используемый метод иссле­дования соотношений частот и разности фаз складываемых колебаний.

11. Термодинамические параметры. Температура. Модель идеального газа.

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ

Молекулярная физика и термодинамика - разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно–кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй - термодинамики.

Молекулярная физика – раздел физики, изучающий строение и свойства вещества исходя из молекулярно – кинетических представлений, основыва-ющихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Идея об атомном строении вещества высказана древнегреческим философом Демокритом (460-370 гг. до н.э.). Атомистика возрождается вновь лишь в XVII в. и развивается в работах М.В.Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р.Клаузиуса, английского физика Дж.Максвелла и австрийского физика Л.Больцмана.

Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете являются свойствами частиц системы, особенностямиих движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т.д.). Например, температура тела определяется скоростью беспорядочного движения его молекул, но т.к. в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.

Термодинамика – раздел физики, изучающий общие свойства макроско-пических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах – фундаментальных законах, установленных в результате обобщения опытных данных.

Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в
которых нельзя было бы пользоваться термодинамическим методом. С другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различными методами исследования.

Термодинамика имеет дело с термодинамической системой – совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Основа термодинамического метода - определение состояния термодинамической системы. Состояние системы задается термодинамическими параметрами (параметрами состояния) – совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и объем.

Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются).

Дата добавления: 2015-08-17