Метод расширенных частотных характеристик

Обычная частотная характеристика отражает свойства исследуемого звена при подаче на вход синусоидальных возмущений с постоянной амплитудой.

или показательной форме:

где, B_ВХ – амплитуда синусоидальных колебаний;

- частота колебаний, рад/с.

Расширенная частотная характеристика отражает свойства объекта (или регулятора) при подаче на вход синусоидальных возмущений с затухающей амплитудой.

где, m – степень колебательности.

Степень колебательности процесса m – характеризует затухание его колебательных составляющих и численно равна абсолютному значению отношения действительной части к коэффициенту при мнимой части корня характеристического уравнения с наименьшим абсолютным значением этого отношения.

, i=1,2,3…;

Между степенью затухания 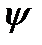и степенью колебательности m существует определенная связь.

Различным значениям степени затухания соответствуют следующие степени колебательности m.

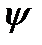
	0,00	0,6	0,75	0,90	0,95
m	0,00	0,414	0,221	0,336	0,478

Расширенные частотные характеристики W(m,j ) получают аналитически из передаточных функций, заменой р на комплексную переменную . При этом степень колебательности m обычно принимают равной 0,221 или 0,366, что соответствует степени затухания процесса 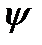, равной 0,75 или 0,9, т.е. затуханию процесса за три или два периода колебаний.

Последовательность определения параметров настройки

Определяется расширенная частотная характеристика

объекта с передаточной функции

или в показательной форме

Определяется расширенная частотная характеристика пропорционально интегрального (ПИ) регулятора с передаточной функцией.

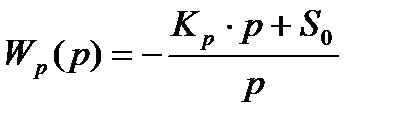
где, К₀ – коэффициент усиления регулятора;

S₀=1/T_И, Т_И – время изодрома регулятора.

Знак минус указывает, что действие регулятора направлено против возмущения.

по показательной форме:

Исходным условием для получения заданной степени колебательности замкнутой системы m, а следовательно, определяемой степени затухания 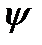является соотношение:

Это соотношение двух комплексных чисел возможно в

том случае, если произведение модулей векторов равно единице, а аргументы (фазы) равны.

Тогда для АСР с ПИ – регулятором получается:

где, - расширенная амплитудно-частотная характеристика объекта;

- расширенная фазо-частотная характеристика объекта;

Решая последние уравнения относительно К_р и S₀, получают:

где,

Задаваясь различными значениями частот , рассчитываются настройки К_р и S₀, строят линию равной степени колебательности и находят визуально из графика значения ^max, а затем _р рабочую частоту и соответствующие ей оптимальные настройки

Плоскость параметров настроек ПИ-регулятора.

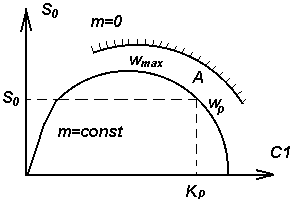
Рис.1.4.

Формулы расчета настроек регулятора с пропорционально- дифференциальным (ПД), пропорциональным (П), пропорционально-интегрально-дифференциальным (ПИД) регуляторами имеют вид:

Пропорциональный (П) регулятор:

Пропорционально-дифференциальный (ПИД) регулятор:

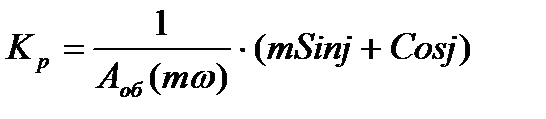
Пропорционально-интегрально-дифференциальный (ПИД) регулятор:

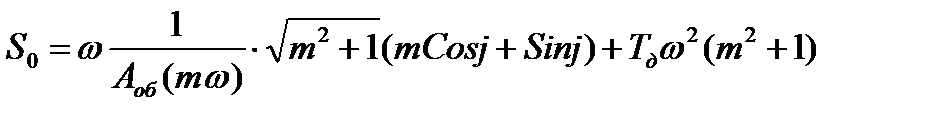
где,

Для построения семейства линии равной m, задается несколько значений затем для каждого значения 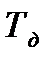при различных значениях находятся условно – оптимальные настройки. Для выбора оптимальной настройки необходимо осуществить моделирование АСР с ПИД регулятором и оценить величину критерия I2.

В качестве оптимальных настроек выбираются настройки той САР, для которой критерий I2 окажется наименьшим.

Пример:

Определить оптимальные настроечные параметры ПИ-регулятора.

Исходные данные: Объект регулирования представлен передаточной функцией апериодического звена:

К₀=571 см/м²; Т₀=3657 с; m=0,221; 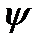=0,75.

Решение:

Расширенная частотная характеристика объекта:

Заменим р на комплексную переменную получаем расширенную амплитудно-фазовую характеристику.

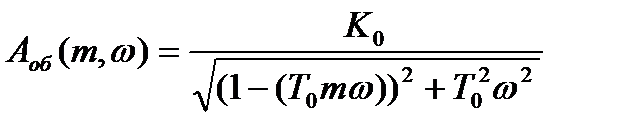
Подставляя численные значения К₀, Т₀ определяем А_об 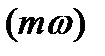при изменении 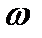от 0 до .

Аоб		6,11	3,06	2,03	1,53	1,27	1,02	0,76	0,51	0,38
		0,025	0,05	0,075	0,1	0,12	0,15	0,2	0,3	0,4
Аоб	0,3	0,25	0,22	0,19	0,15	0,13	0,11	0,1	0,02
	0,5	0,6	0,7	0,8		1,2	1,4	1,6

Определим фазо-частотную характеристику объекта

об		78,18	77,88	77,78	77,73	77,7	77,68	77,65	77,63	77,61
		0,025	0,05	0,075	0,1	0,12	0,15	0,2	0,3	0,4
об	77,6	77,6	77,6	77,59	77,59	77,59	77,59	77,59	77,59
	0,5	0,6	0,7	0,8		1,2	1,4	1,6

Определяем настройки регулятора

(1)

(2)

где,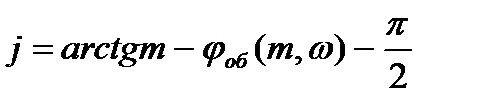

j	-89.78	-88.42	-88.424	-88.426	-88.427	-88.427	-88.429
		0.025	0.05	0.075	0.1	0.12	0.15
j	-88.429	-88.429	-88.429	-88.429	-88.429	-88.429	-88.429
	0.2	0.3	0.4	0.5	0.6	0.7	0.8
j	-88.429	-88.429	-88.429	-88.429	-88.429
		1.2	1.4	1.6

Вычисленные значения подставляем в выражения (1) и (2) составляем таблицу и строем кривую с равной m, по нему находим , а по соотношению , рабочую частоту и соответствующую ей оптимальные настройки ,

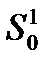
Кр	0,002	0,014	0,149	0,224	0,229
S0		0,0025	0,006	0,008	0,009
		0,025	0,05	0,75	0,1
Кр	0,359	0,45	0,6	0,9	1,2
S0	0,009	0,008	0,005	0,001	0,0004
	0,12	0,15	0,2	0,3	0,4
Кр	1,5	1,8	2,1	2,4
S0	9,58Е-05	1,95Е-05	3,77Е-0,6	6,97Е-07	2,19Е-08
	0,5	0,6	0,7	0,8
Кр	3,6	4,21	4,814
S0	6,32Е-10	1,73Е-11	4,53Е-13
	1,2	1,4	1,6

Рис. 1.5.

Дата добавления: 2015-08-17