Объекта регулирования

ОСНОВЫ РАСЧЕТА ОДНОКОНТУРНОЙ АСР

Задачей расчета автоматической системы регулирования (АСР) является получение переходных процессов системы автоматического регулирования (САР) заданного качества. Качество переходных процессов автоматического регулирования определяется свойствами системы в целом. В свою очередь свойства системы складываются из свойств ее составляющих, т.е. из свойств объекта регулирования и автоматического регулятора. Поскольку объект регулирования является неизменяемой частью системы, то для достижения заданных свойств системы в целом необходимо выбрать соответствующий автоматический регулятор.

Следовательно, с помощью регулятора системе придаются свойства, обеспечивающие заданное качество регулирования. Таким образом, расчет системы автоматического регулирования включает две задачи:

- определение свойств объекта регулирования;

- выбор и расчет автоматического регулятора с такими параметрами, чтобы автоматический регулятор дополнил характеристики объекта регулирования и обеспечил необходимое качество регулирования.

Определение свойств объекта регулирования.

Аналитический метод определения характеристик

объекта регулирования

Процессы, характеризующиеся одной выходной и одной входной величинами могут быть описаны дифференциальным уравнением:

(1)

где, А – постоянный коэффициент, имеющий конкретное значение для того или иного процесса.

- результирующее материальное или энергетическое воздействие на объект.

Выведем дифференциальное уравнение изменения уровня в нижней части колонны.

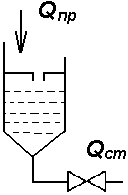
Рис.1.1.

В равновесном состоянии:

При появлении разности уровень будет увеличиваться или уменьшаться.

Если сечение колонны const=F, тогда уравнение (1) для переходного режима примет вид:

(2)

Пусть изменение не зависит от уровня, а - зависит, т.е. при изменении уровня изменяется расход стока. Тогда при небольших изменениях уровня эту зависимость можно записать:

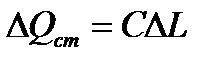(3)

где, С – коэффициент пропорциональности, 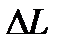- изменение уровня.

Подставляем уравнение (3) в (2) и получим:

постоянная времени объекта:

коэффициент усиления объекта:

(4)

(5)

Характер изменения уровня определяем, решив уравнение:

Характеристическое уравнение соответствующее этому уравнению:

Общее решение уравнения (4):

Частное решение находим из условия равновесия, т.е. когда и

Полное решение уравнения:

Определяем постоянную С из начального условия.

При t=0,

(6)

Как видно из уравнения (4) и (5) динамические свойства объекта соответствуют апериодическому звену.

Пример: Определить численное значение Т₀ и К₀ и построить переходную характеристику для объекта регулирования по (Рис.1.1.).

Дано: F = 8 м²; F0 = 0,002 м² – проходное сечение клапана на стоке; = 0,6 – коэффициент расхода; 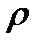= 80 кг/м³ – плотность жидкости; L₃ = 2 м –уровень.

Решение:

Определим объемный расход жидкости через клапан:

учитывая, что Р₂ = 0

,

Подставив исходные данные, получим:

Определим коэффициент пропорциональности С, для этого построим график Q_ст от L.

Н, м	0,5		1,5		2,5
Qст, м^3/с	0,0038	0,0053	0,0065	0,0075	0,0084	0,0092

Рис.1.2.

Практически график имеет линейный характер. Взяв отношение любого значения

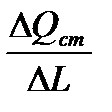
определяем коэффициент пропорциональности С:

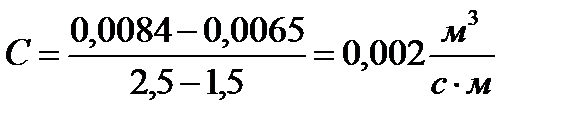
Определяем коэффициент усиления объекта:

Определяем постоянную времени объекта:

Подставим численные значения К₀ и Т₀ в уравнение (6) получим:

По этому уравнению строим переходную характеристику.

Рис.1.3.

Дата добавления: 2015-08-17