
Читайте также:
|
Расчёт на прочность по изгибающему моменту.
Расчёту подлежат балочные пролётные строения железнодорожных мостов из предварительно напряжённого железобетона (типовой проект серии 3.501-81).
Действительную форму поперечного сечения приводим к расчётной форме (рис. 6).
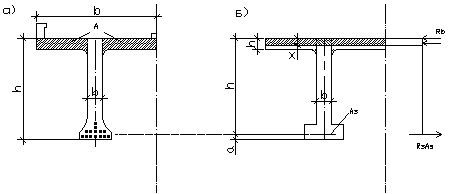
Рис. 6. Расчётная схема поперечного сечения главной балки.
Вычисляем приведённую (среднюю) толщину плиты при фактической ширине плиты bf=2,09 м:

hf’= 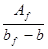 =
= 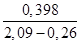 =0,22м.
=0,22м.
Длина свесов плиты между соседними балками не должна превышать 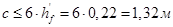 Принимаем c=1,00м.
Принимаем c=1,00м.
Расчётная ширина плиты таврового сечения
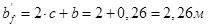
h0=h- as =1,525-0,15=1,375 м
Действительная форма плиты переменной толщины заменяется в расчётном сечении прямоугольной формой с толщиной hf’ и шириной bf’.
Центр тяжести арматуры ориентировочно назначается на расстоянии as=0,15 м от нижней грани пояса балки.
Расчёт на прочность по изгибающему моменту производим, начиная с наиболее нагруженного сечения. Определим в первом приближении высоту сжатой зоны бетона x1 при действии расчётного момента М2=7200,68кН/м:
x1=h0- 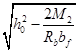 =1,375-
=1,375- 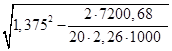 =0,121 м.
=0,121 м.
Так как x1=0,121м < hf’=0,2м, то из этого следует, что cечение рассчитывается как прямоугольное и необходимая площадь рабочей арматуры:
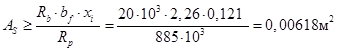
Армирование будем производить высокопрочной проволоки периодического профиля класса Вр-II Æ6 мм c расчётным сопротивлением Rp=885 МПа. Площадь поперечного сечения одной проволоки равна 0,283 см2. Определяем необходимое количество стержней:
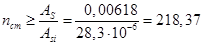
В одном пучке 24 проволоки, следовательно, число пучков равно
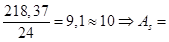 0,00618м2
0,00618м2
Принимаем количество пучков nпуч=10.
После уточнения площади As c учётом принятого количества пучков проволоки находим значение x2:
x2= 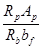 =
=  =0,13м.
=0,13м.
Мпр= Rb* 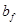 *x2*(h0-0,5x2)
*x2*(h0-0,5x2)  М2
М2
Мпр= 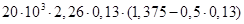 =7697,56
=7697,56  7200,676 кНм
7200,676 кНм
Проверка выполняется, расчёт сечения на прочность по изгибающему моменту закончен.
Расчёт на трещиностойкость в стадии изготовления и эксплуатации.
А. Проверка по образованию нормальных трещин в стадии эксплуатации.
Расчёт производится по наибольшему изгибающему моменту М’’=5015,33кНм от нормативных нагрузок. Предполагается, что на стадии образования трещин бетон и арматура сохраняют упругие свойства. Благодаря предварительному напряжению, конструкция работает полным сечением.
Расчётная форма сечения с основными размерами показана на рис. 8.
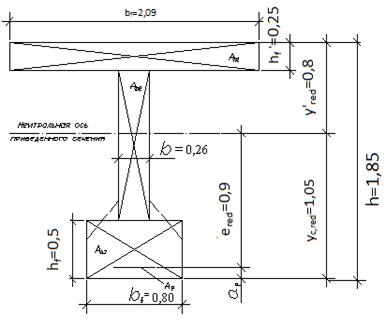
Рис. 8. Схема к расчёту предварительно-напряжённой балки.
Принимаем способ натяжения арматуры – натяжение на упоры. При натяжении арматуры на упоры её сцёпление с бетоном обеспечивается до передачи на конструкцию предварительного натяжения. На всех стадиях изготовления и эксплуатации бетон и арматура в сечениях работают совместно. Определим геометрические характеристики приведённого сечения:
Аb= Аb1+ Аb2+ Аb3=0,497+0,209+0, 400=1,106 м2 - площадь бетонного сечения;
Аb1= h'f*b'f=0,22*2,26=0,497 м2
Аb2=b*(h – hf – h'f)=0,26*(1,525 – 0,5 – 0,22)=0,209 м2
Аb3= hf*bf=0,5*0,8=0,400м2
Sb=Ab1(h-0,5h  )+0,5 Аb2(h-h
)+0,5 Аb2(h-h  +h
+h 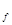 )+0,5 Аb3h
)+0,5 Аb3h 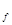 =0,497*(1,525-0,5*0,22)+0,5*0,209*(1,525-0,22+0,5)+0,5*0,4*0,5=0,992 м2 – статический момент бетонного сечения относительно нижней грани балки;
=0,497*(1,525-0,5*0,22)+0,5*0,209*(1,525-0,22+0,5)+0,5*0,4*0,5=0,992 м2 – статический момент бетонного сечения относительно нижней грани балки;
Ared= Аb+n1Ap=1,106 +4,7*0,00618=1,135 м2 – приведённая (с учётом арматуры) площадь поперечного сечения.
Sred=Sb+n1Apap=0,992 +4,7*0,00618*0,15=0,996 м2 – статический момент приведённого сечения относительно нижней грани.
yc,red= 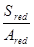 =
= 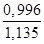 =0,88 м – расстояние до центра тяжести приведённого сечения от нижней грани.
=0,88 м – расстояние до центра тяжести приведённого сечения от нижней грани.
y  =h-y
=h-y 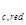 =1,525-0,88=0,645м – расстояние до центра тяжести приведённого сечения от верхней грани.
=1,525-0,88=0,645м – расстояние до центра тяжести приведённого сечения от верхней грани.
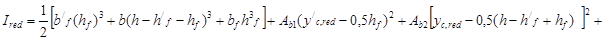

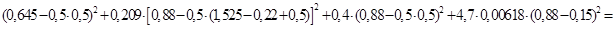 =1,306м4
=1,306м4
момент инерции приведённого сечения относительно нейтральной оси.
Wred=  =
= 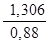 =1,48 м3 – момент сопротивления приведенного сечения относительно нижней грани сечения.
=1,48 м3 – момент сопротивления приведенного сечения относительно нижней грани сечения.
Ожидаемые растягивающие напряжения у нижней грани
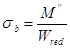 =
= 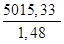 =3388,74кН/м2
=3388,74кН/м2
Предельные растягивающие напряжения в бетоне 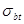 = 0,4
= 0,4 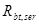 = 0,4*2200= 880 кН/м2.
= 0,4*2200= 880 кН/м2.
Определяем усилие натяжения арматуры N, передаваемое на бетон конструкции:
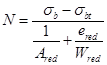 =
= 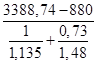 =1825,87 кН,
=1825,87 кН,
где еred = yc,red-ap=0,88-0,15=0,73м – эксцентриситет приложения силы N относительно центра тяжести приведённого сечения.
Установившиеся напряжения в арматуре от её предварительного натяжения
 =
= 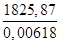 =295,45 МПа.
=295,45 МПа.
Напряжения 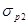 при натяжении арматуры должны быть увеличены с учётом неизбежных потерь напряжений с течением времени от усадки и ползучести бетона, релаксации арматуры и влияния других факторов. Контролируемые при натяжении арматуры напряжения
при натяжении арматуры должны быть увеличены с учётом неизбежных потерь напряжений с течением времени от усадки и ползучести бетона, релаксации арматуры и влияния других факторов. Контролируемые при натяжении арматуры напряжения 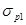 ориентировочно определяются как
ориентировочно определяются как
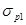 =1,3
=1,3 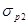 =384,09 МПа
=384,09 МПа  1,1Rp=973,5 МПа.
1,1Rp=973,5 МПа.
Б. Проверка трещиностойкости балки в стадии изготовления.
В стадии изготовления на конструкцию действуют сила предварительного напряжения и собственный вес балки. На этой стадии проверяем в середине пролёта сжимающие нормальные напряжения в крайнем волокне нижнего пояса. Для конструкций с натяжением арматуры на упоры имеем:
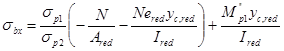

 ,
,
где 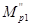 -момент от собственного веса балки в середине пролета
-момент от собственного веса балки в середине пролета
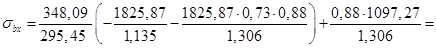 -2,21МПа
-2,21МПа  26 МПа.
26 МПа.
При создании предварительного напряжения в верхней зоне балки могут возникнуть растягивающие напряжения, величина которых для конструкций с натяжением арматуры на упоры определяется как
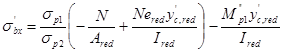
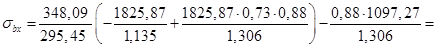
-1,58 МПа  1,76 МПа.
1,76 МПа.
Расчёт на трещиностойкость по касательным и главным напряжениям.
Расчёт производится в стадии эксплуатации на усилия М’’ и Q’’ от нормативных нагрузок и воздействие силы предварительного натяжения N. Предполагается, что в стадии эксплуатации конструкция работает упруго и полным сечением. Напряжения определяются в трёх точках по высоте сечения: в местах примыкания плиты и нижнего пояса к стенке балки и на нейтральной оси.
А. Проверка касательных напряжений.
Расчёт производим для точки, находящейся на нейтральной оси в опорном сечении балки(точка 2 на рис. 10).
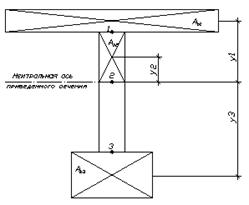
Рис. 10. Схема к расчёту предварительно-напряжённой балки.
Касательные напряжения определяются по формуле
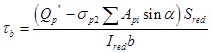
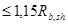 ,
,
Пучки рабочей арматуры отклоним для уменьшения действующей поперечной силы.
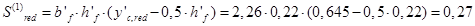 м3
м3
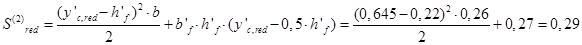 м3
м3
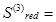 0,252м3
0,252м3
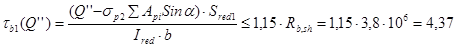 МПа
МПа
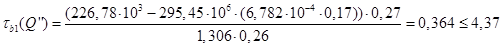 МПа
МПа
 МПа
МПа
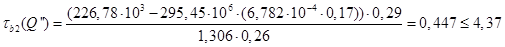 МПа
МПа
 МПа
МПа
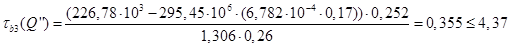 МПа
МПа
По касательным напряжениям на нейтральной оси проверяется принятая толщина стенки балки. Вычисленные значения касательных напряжений используются при определении главных напряжений.
Б. Проверка главных напряжений.
Вычисляются главные растягивающие и главные сжимающие напряжения по формуле
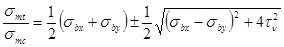
Нормальные напряжения 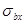 определяются от действия силы предварительного напряжения и изгибающего момента от эксплутационных нагрузок:
определяются от действия силы предварительного напряжения и изгибающего момента от эксплутационных нагрузок:
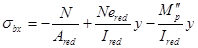
где y – расстояние от нейтральной оси до рассматриваемой точки;
у – имеет положительное значение выше нейтральной оси, отрицательное – ниже нейтральной
оси.
Напряжения 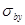 возникают при армировании балки напряжёнными хомутами, в противном случае
возникают при армировании балки напряжёнными хомутами, в противном случае 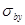 =0.
=0.
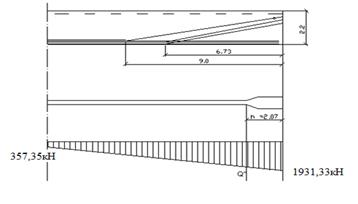
Проверяем главные напряжения в сечении а-а.
Значения момента Мр’’=1097,27 кНм, поперечной силы Qр’’=357,35 кН.
Точка 1.
Вычисляем нормальные напряжения:
 =-1532,02 кН/м2.
=-1532,02 кН/м2.
Вычисляем главные растягивающие напряжения:
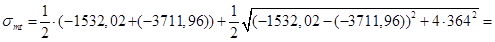 -928,9кН/м2
-928,9кН/м2
Вычисляем главные сжимающие напряжения:
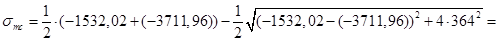 -5175,05кН/м2.
-5175,05кН/м2.
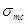 = -5,2МПа
= -5,2МПа 
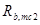 =22,0 МПа.
=22,0 МПа.
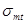 =-0,929МПа
=-0,929МПа  1,496 МПа.
1,496 МПа.
Точка 2.
Вычисляем нормальные напряжения:
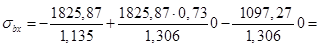 -1608,76кН/м2.
-1608,76кН/м2.
Вычисляем главные растягивающие напряжения:
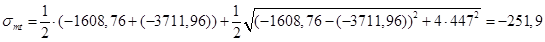 кН/м2.
кН/м2.
Вычисляем главные сжимающие напряжения:
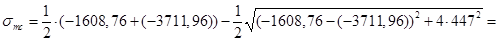 = -5528,5кН/м2.
= -5528,5кН/м2.
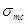 =-5,529МПа
=-5,529МПа 
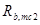 =22,0 МПа.
=22,0 МПа.
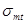 =-0,252МПа
=-0,252МПа  1,496 МПа.
1,496 МПа.
Точка 3.
Вычисляем нормальные напряжения:
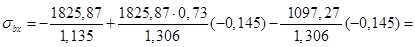 1634,86кН/м2.
1634,86кН/м2.
Вычисляем главные растягивающие напряжения:
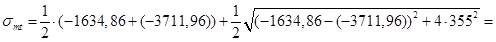 363,38кН/м2.
363,38кН/м2.
Вычисляем главные сжимающие напряжения:
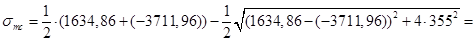 -5795,98кН/м2.
-5795,98кН/м2.
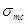 =-5,8 МПа
=-5,8 МПа 
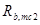 =22,0 МПа.
=22,0 МПа.
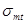 =0,363МПа
=0,363МПа  1,496 МПа.
1,496 МПа.
Расчёт на прочность по поперечной силе.
Расчёт производится в сечении, образованном наклонной трещиной. Поперечная сила воспринимается отклонёнными пучками напряжённой арматуры, хомутами и бетоном сжатой зоны сечения. Определим распределённую поперечную нагрузку, воспринимаемую хомутами в наклонном сечении:
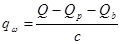 ,
,
где Q=1516,42 кН – поперечная сила в рассматриваемом сечении;
Qp=  =619500(
=619500(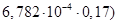 =123,64 кН - проекция усилия в отклонённых пучках на вертикальную ось;
=123,64 кН - проекция усилия в отклонённых пучках на вертикальную ось;
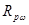 =0,8Rр=619,5МПа – расчётное сопротивление отклонённых пучков;
=0,8Rр=619,5МПа – расчётное сопротивление отклонённых пучков;
Qb= 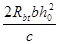 =
= 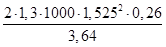 =431,9 кН – проекция усилия в бетоне сжатой зоны сечения на вертикальную ось;
=431,9 кН – проекция усилия в бетоне сжатой зоны сечения на вертикальную ось;
с=3,64 м – длина горизонтальной проекции наклонного сечения, определяемая из условия, что угол наклона сечения к продольной оси балки составляет 30 градусов.
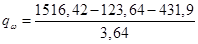 =263,98 кН/м.
=263,98 кН/м.
Прочность хомутов обеспечивается при выполнении условия
 ,
,
где 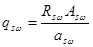 =66,32кН/м – предельное усилие на единицу длины в обычных хомутах;
=66,32кН/м – предельное усилие на единицу длины в обычных хомутах;
 - предельное усилие на единицу длины в напряжённых хомутах;
- предельное усилие на единицу длины в напряжённых хомутах;
 =908,34 кН/м- предельное усилие на единицу длины в напряженных хомутах;
=908,34 кН/м- предельное усилие на единицу длины в напряженных хомутах;
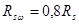 =264 МПа – расчётное сопротивление обычных хомутов;
=264 МПа – расчётное сопротивление обычных хомутов;
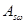 =
=  =2*
=2* 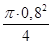 =1,0 см 2 – площадь всех ветвей обычного хомута;
=1,0 см 2 – площадь всех ветвей обычного хомута;
Назначаем диаметр обычных хомутов 10 мм и принимаем шаг обычных хомутов  =20см.
=20см.
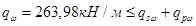 =908,33+66,32=974,65 кН/м.
=908,33+66,32=974,65 кН/м.
Прочность хомутов обеспечена.
Нижний пояс предварительно-напряжённой балки армируем замкнутыми хомутами того же диаметра, что и хомуты стенки, шаг замкнутых хомутов принимаем равным 15 см.
Дата добавления: 2015-08-17; просмотров: 134 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение расчётных усилий. | | | НАХЛЫСТОВАЯ СНАСТЬ |