
Читайте также:
|
С помощью определенного интеграла можно также вычислять площади плоских фигур, так как эта задача всегда сводится к вычислению площадей криволинейных трапеций.
Площадь всякой плоской фигуры в прямоугольной системе координат может быть составлена из площадей криволинейных трапеций, прилегающих к оси  или
или 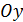 . Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:
. Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:
1. По условию задачи делают схематический чертеж.
2. Представляют искомую площадь как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.
3. Записывают каждую функцию в виде 
4. Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.
Площади фигур, расположенных над осью 
Пример1. Вычислить площади фигур, ограниченных заданными линиями: 
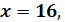 x = 25, и y = 0 (рис.4)
x = 25, и y = 0 (рис.4)
Решение. Для любого  функция
функция  принимает положительные значения; поэтому для вычисления площади данной криволинейной трапеции следует воспользоваться формулой
принимает положительные значения; поэтому для вычисления площади данной криволинейной трапеции следует воспользоваться формулой
 =
=  dx =
dx = 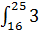 x1/2
x1/2 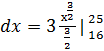 = 2
= 2 
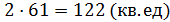

Рис.4
Площади фигур, расположенных полностью или частично под осью 
Пусть на отрезке [a,b] задана неположительная непрерывная функция  .
.
Если фигура, расположенная под осью ОХ, является криволинейной трапецией, то её площадь вычисляется по формуле
 или
или 
где 
Пример 2. 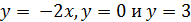
Решение: На отрезке [0,3] функция 

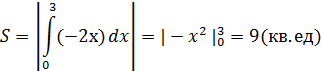
Пусть функция 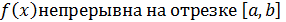

 отрицательные значения. Тогда нужно разбить отрезок [a,b] на такие части, в каждой из которых функция не изменяет знак, затем по приведенным выше формулам вычислить соответствующие этим частям площади и найденные площади сложить.
отрицательные значения. Тогда нужно разбить отрезок [a,b] на такие части, в каждой из которых функция не изменяет знак, затем по приведенным выше формулам вычислить соответствующие этим частям площади и найденные площади сложить.
Пример 3. 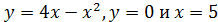
Решение: Парабола 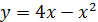 пересекает ось абсцисс в точках
пересекает ось абсцисс в точках 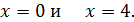 Фигура, площадь которой требуется найти, отмечена цветом на рисунке 5.
Фигура, площадь которой требуется найти, отмечена цветом на рисунке 5.
рис.6 рис.7 


рис. 5
Пусть S1 и S2 - площади частей этой фигуры, соответствующих отрезкам[0,4] и [4,5], а S- искомая площадь; тогда S=S1 + S2.
 (кв.ед)
(кв.ед)

Следовательно, S=  =13(кв.ед)
=13(кв.ед)
Площади фигур, прилегающих к оси 
Если криволинейная трапеция прилегает к оси ординат и ограничена непрерывной кривой  , то ее площадь вычисляется по формуле
, то ее площадь вычисляется по формуле
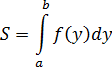
Пример 4. 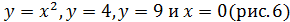
Решение. Данная фигура есть криволинейная трапеция, прилегающая к оси 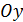 . Пределами интегрирования по
. Пределами интегрирования по  являются значения
являются значения  Запишем данную функцию в виде
Запишем данную функцию в виде  .
.
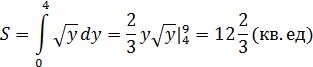
Дата добавления: 2015-08-17; просмотров: 280 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Подстановка в определенном интеграле | | | Симметрично расположенные плоские фигуры |