Расчет главной балки пролетного строения.

2.2.1. Определение расчетных усилий.

Постоянная нагрузка на пролетное строение складывается из собственного веса конструкции и веса мостового полотна.

Нормативная нагрузка на 1 погонный метр главной балки, кН/м, определяется:

- от собственного веса

=

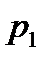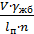
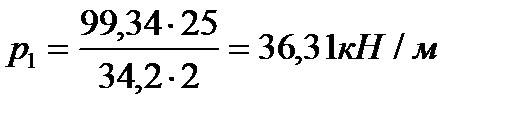
- от веса мостового полотна с ездой на балласте

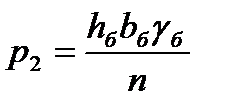
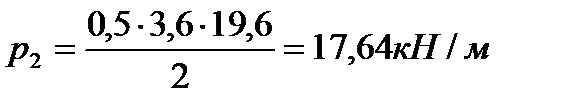
где γ_жб, γ_б – удельный вес ж/б и балласта соответственно;

h_б – толщина слоя балласта;

b_б – ширина балластного корыта, обычно принимаемая для однопутных

мостов равной 3.6м.

Нормативная временная нагрузка по схеме СК используется в виде:

- эквивалентной нагрузки 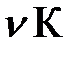кН/м, соответствующей наиболее тяжелой нагрузке от состава с локомотивом;

- распределенной нагрузки 9.81К кН/м от веса груженых вагонов состава;

- нагрузки 13.7 кН/м от порожнего подвижного состава.

Однозначные линии влияния и отдельные участки двузначных линий влияния загружаются эквивалентной нагрузкой 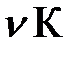. Нормативная временная вертикальная нагрузка на одну главную балку принимается равной

,

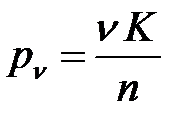где 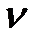- эквивалентная нагрузка класса К=1;

К- класс заданной нагрузки.

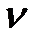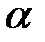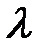Интенсивность эквивалентной нагрузки зависит от параметров и , определяющих положение вершины и длину загружения участка линии влияния (при устройстве пути на балласте α=0,5 при λ≤10м).

Рис. 8 Линии влияния усилий в разрезной балке

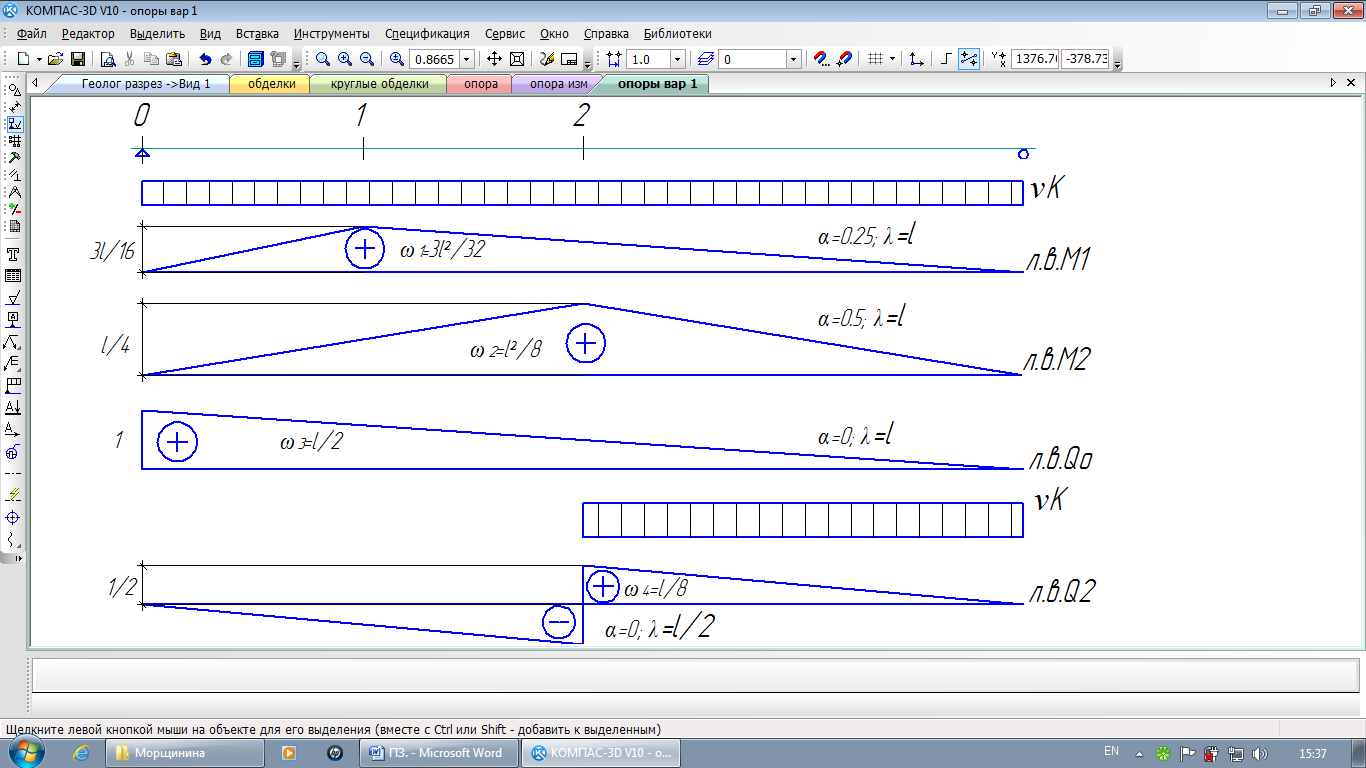
Усилие	α	λ	ν	рν	ω	γfν	1+μ
М1	0,25	33,5	11,89	71,34	105,21	1,20	1,19
М2	0,5	33,5	11,10	66,60	140,28	1,20	1,19
Q0		33,5	12,68	76,08	16,75	1,20	1,19
Q2		16,75	15,48	92,88	4,19	1,25	1,27

Динамический коэффициент к нагрузкам от подвижного состава определяется по формуле и принимается не менее 1,15:

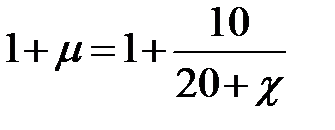
где χ– длинна расчетного пролета l_р.

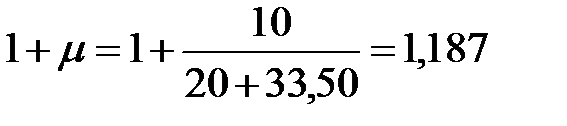
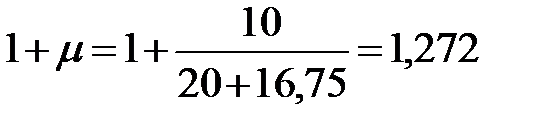
Полные усилия в сечениях разрезной балки при расчете на прочность определяются с учетом всех требований по следующим формулам:

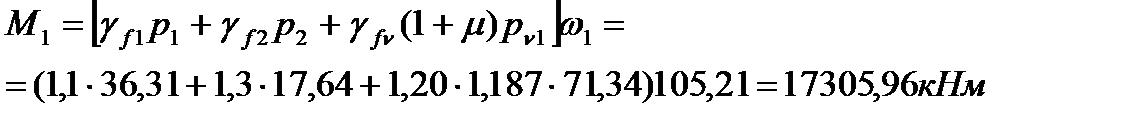
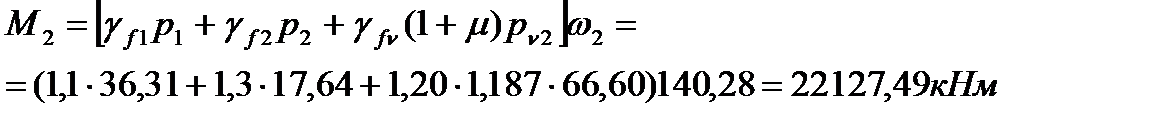
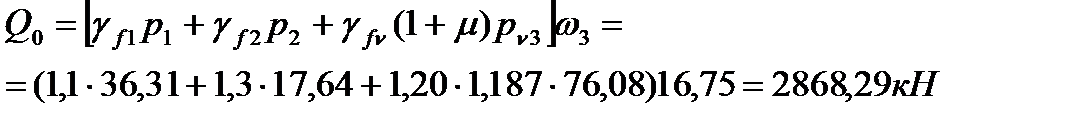
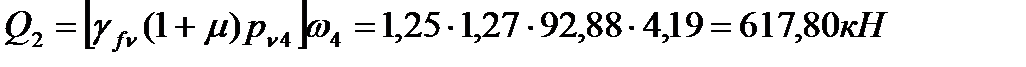
Строим огибающие эпюры действующих в конструкции усилий:

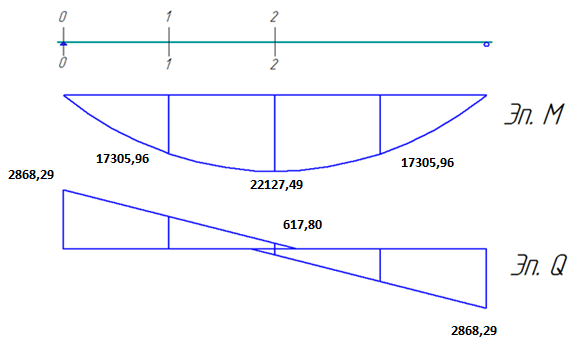
Рис. 9 Огибающие эпюры в разрезной балке

Усилия на трещиностойкость определяются от действия на конструкцию нормативных нагрузок. Коэффициенты надежности по нагрузке и динамический коэффициент принимаются равными 1.

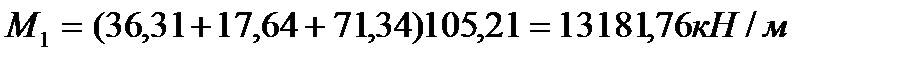
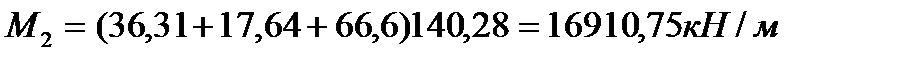
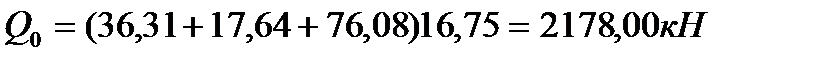
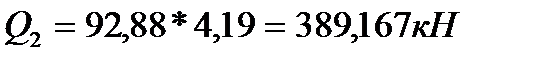
2.2.2. Расчет балки таврового сечения из обычного железобетона.

Приводим действительную форму поперечного сечения к расчетной:

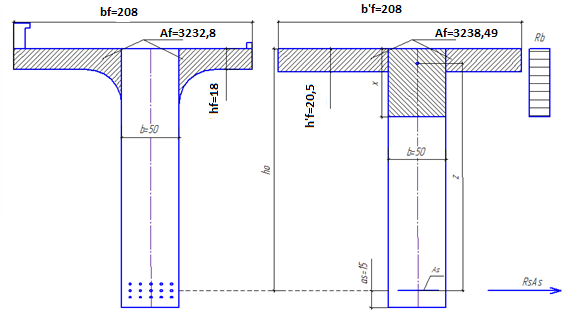
Рис. 10 Расчетные схемы поперечных сечений главной балки

Расчет на прочность по изгибающему моменту.

Расчет ведется по наиболее нагруженному сечению (2-2).

Высота сжатой зоны бетона при действии максимального расчетного момента:

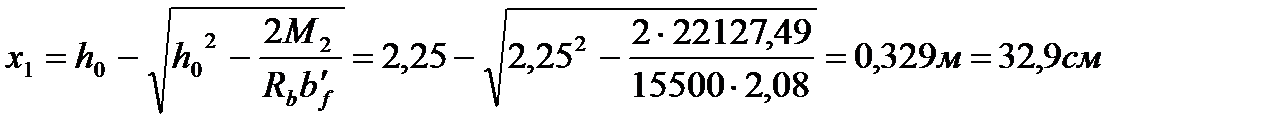
Так как x₁>h’_f значит,что в сжатую зону,кроме плиты, входит часть ребра главной балки, и сечение рассчитывается как тавровое.

M_i=M_i’+M_i”

M_i’=R_b(b_f’-b)h_f’(h₀-0,5 h_f’)=10781,42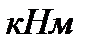

M_i”= M_i- M_i’=11346,07

Находим высоту сжатой зоны в ребре.

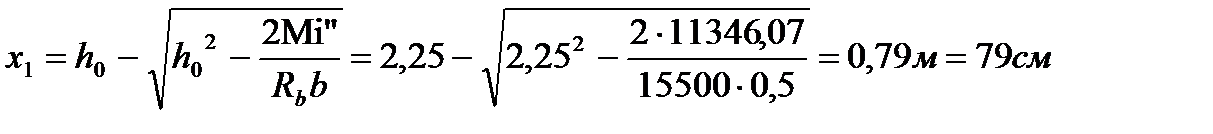
Плечо пары внутренних сил таврового сечения

Z = 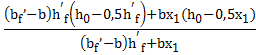= 1,99 м

Определяем необходимую площадь рабочей арматуры:

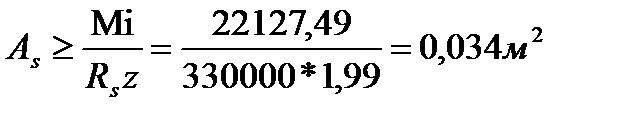
Принимаем арматуру класса АIII диаметром 40мм и определяем количество стержней:

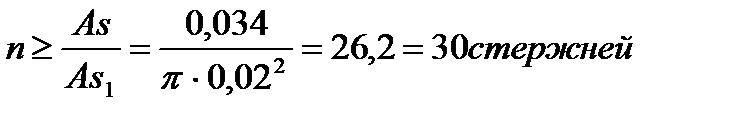
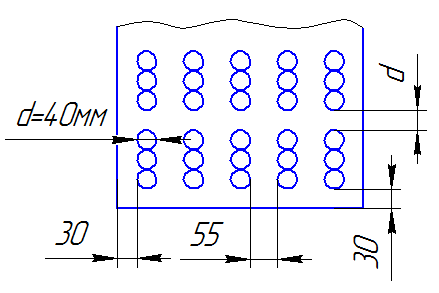
Рис. 11Размещение рабочей арматуры каркасами в балках из обычного железобетона

После уточнения площади As с учетом принятого диаметра и количества стержней арматуры находим значение х₂:

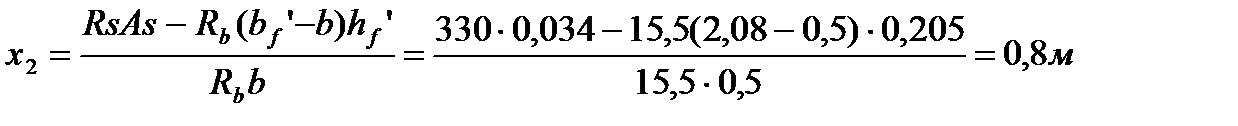
Плечо пары внутренних сил таврового сечения:

Z = 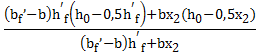= 1,984 м

Определяем предельный момент:

М_пр=R_sA_sz=330000∙0,034∙1,984=22260,48 кНм.

Условие прочности по изгибающему моменту выполнено:

М_пр=22260,48 ≥ М₂=22127,49.

2.2.3 Расчет на трещиностойкость по касательным напряжениям

Расчет по касательным напряжениям выполняют в предположении упругой работы конструкции, но без учета растянутой зоны. В расчете ограничивается величина касательных напряжений действующих по нейтральной оси сечения.

Касательные напряжения определяем приближенно по формуле:

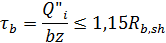
где 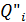- поперечная сила в рассматриваемом при опорном сечении от нормативных нагрузок;

b - толщина ребра балки;

z - плечо пары сил из расчета на прочность по изгибающему моменту.

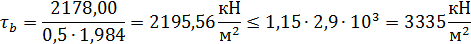
Условие выполняется.

2.2.4. Построение эпюры материалов

.

При расчете изгибаемых элементов на прочность по поперечной силе предполагается, что в предельном состоянии образуется наклонная трещина в бетоне, разделяющая элемент на две части. Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны.

Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих моментов. Для этого точки отгибов сносим на эпюру М, следя за тем, чтобы предельный момент для оставшихся стержней рабочей арматуры не был меньше расчетного момента в сечении. Эпюра предельных моментов (эпюра материалов) должна быть во всех сечениях объемлющей по отношению к эпюре расчетных моментов. Для построения эпюры материалов используем приближенную зависимость, считая, что предельный момент, воспринимаемый сечением с одним стержнем рабочей арматуры, равен:

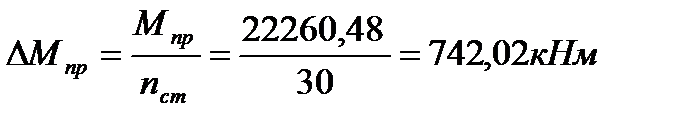
где n_ст – количество стержней рабочей арматуры в среднем сечении.

Графически 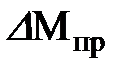получаем делением максимальной ординаты горизонтальными линиями на равные отрезки, число которых соответствует количеству стержней рабочей арматуры. Точки пересечения горизонтальных линий с эпюрой расчетных моментов определяет места возможного отгиба стержней. Наклонные стержни должны равномерно армировать ребро главной балки. На всем участке расположения отогнутой арматуры любое произвольно выбранное вертикальное сечение должно пересекать хотя бы один наклонный стержень. Угол наклона стержней 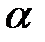к оси балки принимаем равным 30^о.

Не менее 1/3 стержней рабочей арматуры должны доводиться без отгибов до опоры (в нашем случае это 10 стержней).

Рис. 12 Эпюра материалов

2.2.4. Расчет на прочность наклонного сечения.

На действие поперечной силы.

Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны.Проверка производится из условия:

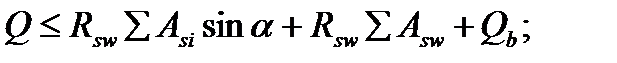
где: Q – максимальное значение поперечной силы от внешних нагрузок, расположенных по одну сторону от наклонного сечения;

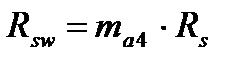– расчетные сопротивления отогнутых стержней и хомутов с учетом коэффициента условия работы арматуры 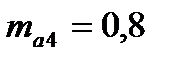(п. 3.40* СНиП 2.05.03-84*);

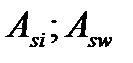– площадь поперечного сечения отогнутого стержня и вспех ветвей одного хомута, пересекающих наклонное сечение;

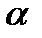– угол наклона стержней к продольной оси элемента;

Для приопорной части длина горизонтальной проекции сечения определяется по формуле:

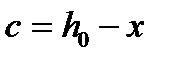
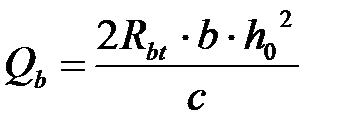– поперечное усилие, передаваемое в расчете на

бетон в сжатой зоне под концом наклонного сечения.

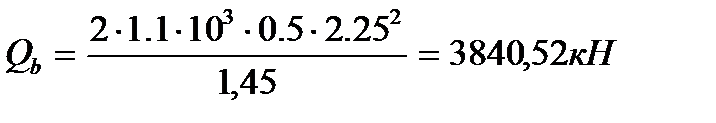
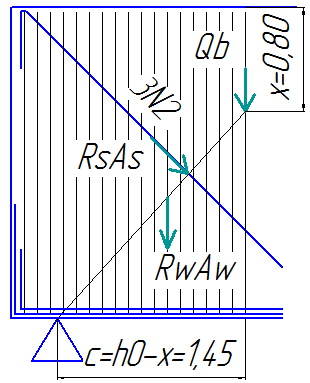
Рис. 13 Схема усилий в сечении при расчете его на прочность

на действие поперечной силы

Располагая схемой размещения арматуры, определяем количество стержней, пересекающих наклонное сечение. Затем находим суммарные площади их сечений.

Наклонное сечение пересекают 3 отогнутых стержней (диаметр 40 мм) и 15 хомутов (диаметр 10 мм).

Таким образом, получаем

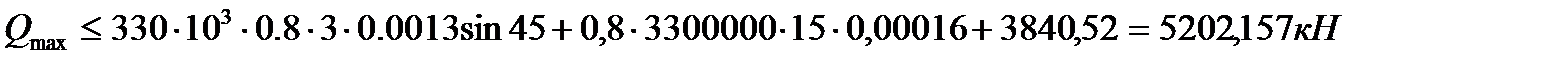
Прочность наклонного сечения на приопорном участке по поперечной силе обеспечена с большим запасом.

2.2.5. Расчет по II предельному состоянию

Расчет сечений наклонных к продольной оси элемента на действие

изгибающих моментов

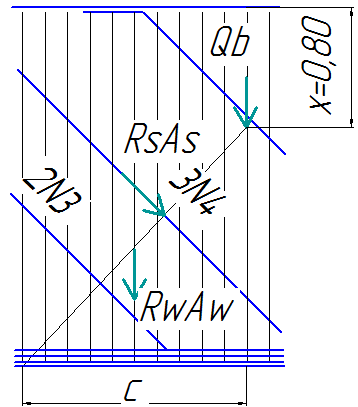
Рис. 14 Схема усилий в сечении при расчете его на прочность на действие изгибающего момента.

Проверка производится из условия:

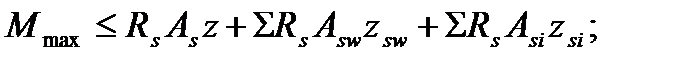
где: 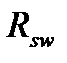– расчетные сопротивления отогнутых стержней и хомутов;

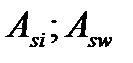– площадь поперечного сечения отогнутых стержней и хомутов;

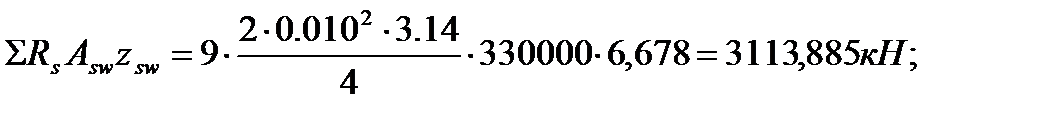
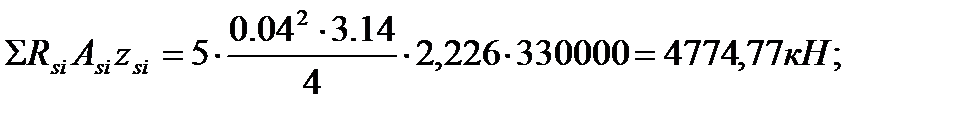
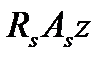=330000 0,034 1,984=22260,48 кН;

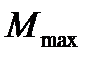
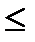3113,885+4774,77+22260,48=30149,13

Условие выполняется.

Определение прогиба.

Расчет по общим деформациям главных балок сводится к определению фактических значений прогибов и сравнению их с допустимыми.

В курсовом проектировании допускается использовать простую формулу для определения вертикального упругого прогиба для балки на двух опорах.

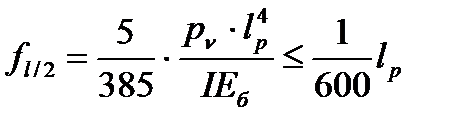
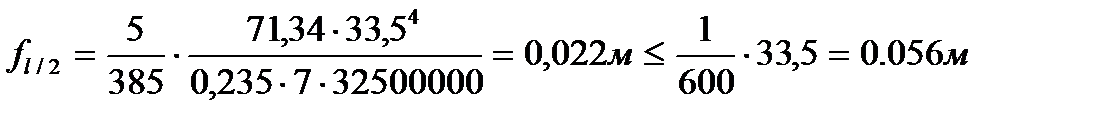
Условие выполнено.

Проверка трещиностойкости.

В зависимости от вида, назначений и условий работы мостовые сооружения и их элементы подразделяются на три категории по трещиностойкости. Мостовые конструкции из ненапрягаемого железобетона относятся к категории 3в. Предельное значение расчетной ширины раскрытия трещин для категории 3в равно 0.02см.

Ширину раскрытия нормальных и наклонных к продольной оси элемента трещин определяем по формуле:

,

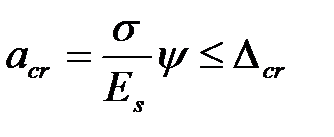где 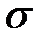- растягивающее напряжение, равное для ненапрягаемой арматуры напряжению 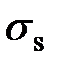в наиболее растянутых стержнях;

;

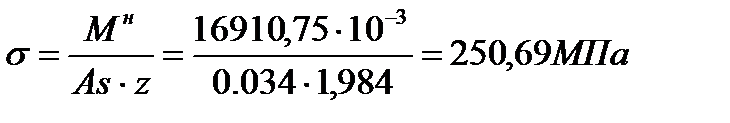E_s – модуль упругости для ненапрягаемой арматуры; Е_s=1.96∙10⁵МПа;

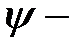коэффициент раскрытия трещин, определяемый в зависимости от

радиуса армирования:

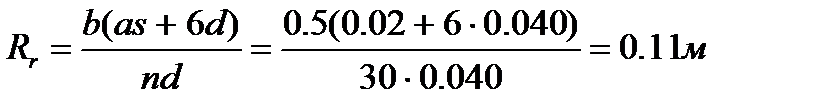
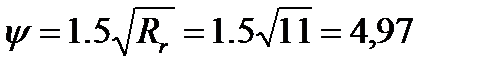
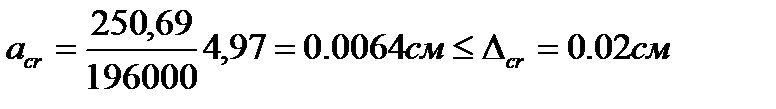
Условие выполнено.

СПИСОК ЛИТЕРАТУРЫ

1. СНиП 2.05.03 - 84 " Мосты и трубы".

2. Круглов В.М. “Методические указания к курсовой работе по мостам”. Новосибирск: изд-во СГУПСа, 2001 г–35 с.

3. Другов Л.И. “Разработка вариантов моста и путепровода под железную дорогу”. Гомель: БелИИЖТ, 1985 г. – 35 с.

4. Карапетов Э.С. “Расчет балочных пролетных строений железобетонных мостов”. Санкт-Петербург, 2004 г. – 50 с.

Дата добавления: 2015-08-17