ГЛАВА 18. Особенности расчета транспортных сооружений в городах

Особенности расчета транспортных сооружений в городах

Особенности расчета эстакад сложного очертания в плане

Расчет эстакад в современных условиях производят в основном на основе метода конечных элементов (МКЭ), что позволяет в значительной степени уменьшить трудозатраты проектировщиков при одновременном получении подробных результатов во всех интересующих сечениях и узлах пролетных строений и опор. Учи­тывая, что в городских условиях эстакады имеют обычно сложное очертание, применение МКЭ является по сути единственной воз­можностью.

В мировой практике существует большое разнообразие программ расчета и проектирования, базирующихся на аппроксимации не­сущих конструкций стержнями, плоскими и объемными коне­чными элементами (рис. 18.1).

Задача расчета по МКЭ сводится в общем случае к составле­нию и решению систем линейных алгебраических уравнений вида

{К_р} = 0, (18.1)

где [К] — матрица единичных коэффициентов метода перемеще­ний; {К_р} и {2} — векторы реакций Гу в заделках по направлению г от внешней нагрузки Р и искомых перемещений %.

С помощью комбинации конечных элементов и с единых мето­дологических позиций могут быть аппроксимированы и рассчита­ны самые разнообразные по геометрии пространственные конст­рукции пролетных строений эстакад с наиболее полным отраже­нием специфических свойств железобетона под действием раз­личных постоянных и временных нагрузок.

Выбор расчетной модели МКЭ для сложных мостовых конст­рукций является непростой задачей, при решении которой во многих случаях требуются теоретические и экспериментальные исследования.

Один из наиболее известных способов задания пространствен­ной мостовой конструкции является ее представление в виде ка­кого-то количества точек в пространстве, соединенных в опреде­ленном порядке. Эти точки могут соединяться криволинейными или прямыми линиями. Пространственные точки могут быть лю­быми особыми точками конструкции: перелома осей, разветвле­ния, прикрепления связей и опирания и т.д. Линии, соединя-

ющие эти точки, также могут быть любыми пространственными кривыми, представляющими собой оси элементов конструкции, проходящие через центры тяжести сечений, а также оси, прохо­дящие через центры изгиба или какие-либо другие заданные то­чки сечений, и т.п.

Задание конструкции и анализ ее схемы значительно упроща­ются, если принимаются следующие дополнительные условия:

• все точки конструкции с координатами в пространстве со­
единяются прямыми линиями;

• соединения элементов конструкции, не передающие какое-
либо усилие, и опорные закрепления моделируются шарнирно-
подвижными связями, причем в месте их прикрепления шарнир
перерезает сходящиеся к нему элементы;

• во всех точках системы сходящиеся в них элементы конструк­
ции считаются жестко соединенными, передающими все виды
силовых воздействий.

Порядок расчета сооружений по такой модели разбивается на три основные этапа:

1) подготовительный этап, включающий в себя изображение расчетной схемы рассматриваемого сооружения, разбиение рас­четной схемы на отдельные элементы, нумерацию узлов и эле­ментов, выбор общей системы осей координат. Затем составляют­ся исходные матрицы жесткости отдельных элементов в местной

в

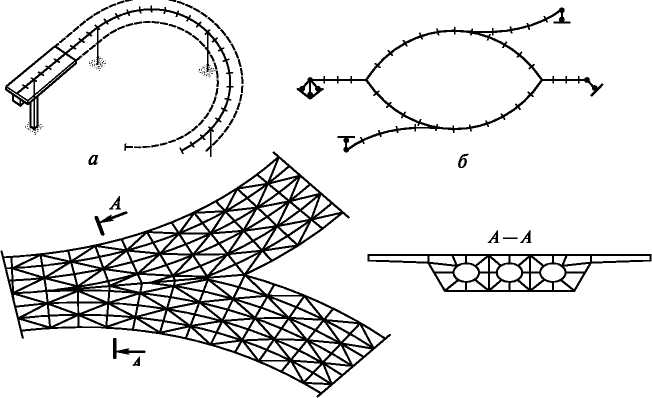
Рис. 18.1. Идеализация пролетных строений криволинейных эстакад ко­нечными элементами:

а — в виде пространственных блоков пролетного строения; б — стержнями; в — пространственными элементами

системе осей координат [к]' и матрицы направляющих косинусов [с], формируется вектор внешних нагрузок {Р} после предвари­тельного преобразования внеузловых нагрузок к узловым;

2) вычислительная часть расчета включает в себя определение
матрицы жесткости отдельных элементов в общей системе осей
координат [к] = [с]^т [к]' [с] и последующее формирование матрицы
жесткости [К] для сооружения в целом. По формуле {А} = [Щ~¹ {Р}
вычисляют вектор перемещений узловых точек сооружения в об­
щей системе осей координат;

3) от вектора перемещений производится переход к деформа­
циям, а от них — к усилиям и напряжениям.

Более подробно теория расчета по МКЭ и другими численным методам приведена в учебной и специальной литературе.

Для предварительной оценки напряженно-деформированного состояния криволинейных пролетных строений эстакад возможно использование и более приближенных методик, учитывающих многообразие силовых и деформационных факторов.

Криволинейные и косые пролетные строения можно рассмат­ривать как брусья или тонкостенные стержни с недеформируемым или деформируемым контуром поперечного сечения. Для таких случаев разработаны соответствующие методики, позволяющие получать усилия, линейные и угловые перемещения, необходи­мые для проектирования. Для различных случаев закрепления кри­волинейных брусьев по концам и кривизне имеются таблицы, значительно упрощающие приближенный расчет.

Дата добавления: 2015-08-17