Анализ системы автоматического управления

а. Исследование заданной системы на устойчивость двумя критериями

Исходная схема содержит следующие типовые динамические звенья: апериодические звенья: K₁/(T₁p+1); K₂/(T₂p+1); K₅/(T₅p+1); и колебательное звено второго порядка К₃/(Т₃²р²+Т₄р+1). Найдём передаточную функцию для разомкнутой системы (когда отсутствует отрицательная обратная связь с выхода y).

Выполним преобразования:

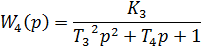
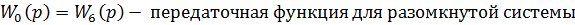
Предварительно проверим на устойчивость разомкнутую систему. Для этого найдем корни характеристического уравнения:

Все корни имеют отрицательную вещественную часть. Следовательно, разомкнутая система устойчива. Запишем выражение для обобщенной частотной характеристики разомкнутой системы. Для этого введем замену переменных , где - частота, изменяющаяся в некоторых пределах, и выполним построение графика:

Рисунок 2. Амплитудно-фазовая характеристика разомкнутой системы

Построенная характеристика охватывает точку с координатами , а следовательно рассматриваемая система неустойчива.

Рисунок 3. Логарифмические частотные характеристики разомкнутой системы

Построенная характеристика показывает, что не на всех частотах, при которых ЛАЧХ положительна, фазовый сдвиг не достигает значения . Следовательно, рассматриваемая система неустойчива.

Проверим систему на устойчивость с помощью критерия Гурвица. Запишем передаточную функцию для замкнутой системы:

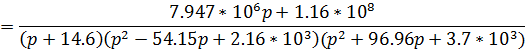
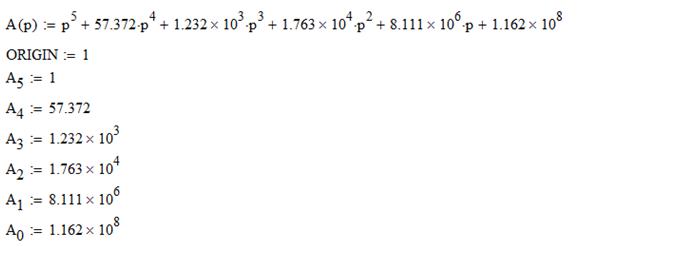
Составим матрицу Гурвица:

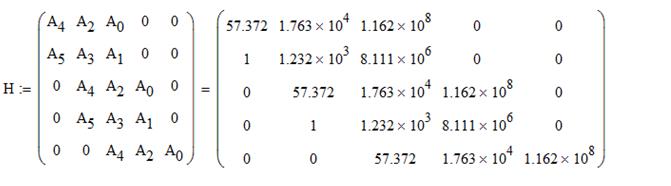
Таким образом, по критерию Гурвица видим, что определитель , а следовательно рассматриваемая система неустойчива как по критерию Гурвица, так и по критерию Найквиста.

б. Определение ошибки заданной САУ в установившемся режиме.

Так как рассматриваемая система неустойчива, то нет необходимости определять ошибку в установившемся режиме

Дата добавления: 2015-08-17