Верхние и нижние линии тока

Построим две другие линий тока. Обозначим функцию тока для той из них, которая проходит выше основной, , а для той, что ниже, .

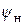Как известно, разность значений функции тока на соседних линиях тока определяет объемный расход несжимаемой жидкости в слое единичной толщины между ними:

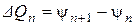. (18)

Картина течения будет наглядной, если 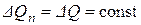. Тогда во всей области течения расстояние по нормали между соседними линиями тока будет обратно пропорционально скорости течения. Объемный же расход удобно выразить через расстояние между соседними линиями тока на бесконечном удалении от цилиндра: .

Уравнение верхней линии тока. Вдоль верхней линии тока должно соблюдаться условие . Определим эту константу из выражения (18), откуда с учетом того, что , следует

(19)

Подставляя в левую часть равенства (19) общее выражение для функции тока (9), получим

(20)

Правую часть формулы (20) можно записать в виде одного слагаемого. Для этого введем постоянную величину 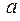, которую определим следующим образом:

(21)

Эта величина зависит от условий задачи и от выбора значения . Из (21) следует

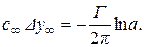(22)

Подставим (22) в (20) и заменим сумму логарифмов в правой части формулы логарифмом произведения. Тогда значение константы для верхней линии тока примет вид

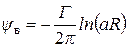. (23)

Проводя далее преобразования, аналогичные тем, которые были выполнены в формулах (14) – (16), для верхней линии тока получим

(24)

где

Заметим, что если в формулу (21) вместо подставить N , где N – любое целое число, то можно вывести формулу для построения всего множества линий тока, расположенных выше основной.

Уравнение нижней линии тока. Проделав аналогичные выкладки с учетом того, что для нижней линии тока величина станет отрицательной, найдем

(25)

Техника построения верхней, нижней и основной линий тока одна и та же. Разница лишь в установлении нижнего предела области допустимых значений задаваемых в расчете независимых переменных и . Очевидно, что для основной линии тока построение надо начинать с полярного радиуса, равного радиусу цилиндра. Этому радиусу соответствуют критические точки, лежащие на поверхности цилиндра: . Для верхней и нижней линий тока минимальные значения и необходимо найти заранее, чтобы уверенно построить верхнюю и нижнюю линии тока вблизи поверхности цилиндра.

Определим минимальный полярный радиус-вектор верхней линии тока , т. е. минимальное расстояние от начала координат до точки, принадлежащей верхней линии тока (см. рис. 1). Минимально удаленная от начала координат (и от поверхности цилиндра) точка располагается на оси ординат. Полярный угол, соответствующий положению этой точки, равен . Для нахождения в выражение (24), описывающее координаты всех точек верхней линии тока, в том числе и минимально удаленной от начала координат точки, подставим значение . После подстановки получим уравнение относительно минимального верхнего радиус-вектора :

(26)

Соотношение (26) дает решение для в неявном виде. Корень этого уравнения можно найти, например, графически. Для этого нужно построить функции, стоящие слева и справа от знака равенства:

(27)

Значения аргумента должны быть больше единицы в безразмерных координатах, поскольку верхняя линия тока нигде не касается цилиндра, и расстояние от ее точек до начала координат всегда больше . Шаг изменения аргумента при построении должен быть малым, а масштаб графика – большим, чтобы получить приемлемую точность решения. Построив графики функций и , найдем точку их пересечения, где f ₁ = f ₂. Значение в этой точке – корень уравнения (26).

Аналогичным образом определяется значение 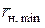для нижней линии тока. Необходимо только иметь в виду, что для определения 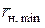надо использовать не уравнение (24), а уравнение (25) и что положение 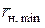определяется углом . При этом вместо уравнений (27) получим

(28)

Все три функции f ₁, f ₂, и f ₃ можно построить на одном графике (рис.2).

Дата добавления: 2015-08-20