Основная линия тока

Обозначим величину функции тока (значение константы) на основной линии тока . Поскольку основная линия тока частично совпадает с поверхностью цилиндра, константу в уравнении линии тока можно определить из условия, что на участке АВ полярный радиус r совпадает с радиусом цилиндра (r = R).

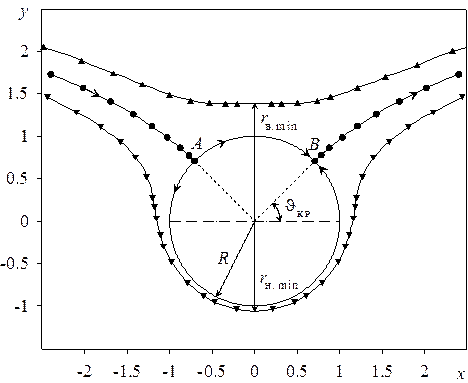
Рис. 1. Линии тока: ▲ – верхняя, l – основная, ▼ – нижняя

Подставив r = R в общее выражение для линии тока (9) и упростив результат, получим

(13)

Стоящее справа от второго знака равенства выражение и является значением искомой константы на основной линии тока*. Тогда согласно формуле (9) уравнение этой линии тока, описывающее все ее точки (не только лежащие на поверхности цилиндра) имеет вид:

(14)

Преобразуем выражение (14), перенеся из левой части в правую слагаемое с логарифмом; разность же логарифмов заменим логарифмом дроби и разделим обе части равенства на выражение, стоящее в круглых скобках:

. (15)

Воспользовавшись связью между циркуляцией и положением критических точек (12) и введя безразмерный полярный радиус , окончательно получим

. (16)

Формула (16) может быть использована для построения по точкам основной линии тока. Для этого нужно задать значение безразмерного радиуса, подставить его в правую часть равенства (16) и вычислить ,а затем – значение угла .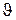

Положение точки на плоскости в полярных координатах полностью определяется углом, отсчитанным от положительной полуоси абсцисс, и расстоянием от начала координат (модулем полярного вектора). Таким образом, знание и 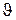позволяет нанести на координатную плоскость точку, принадлежащую основной линии тока. Задавая различные расстояния от начала координат (величины полярного вектора), можно построить множество точек, принадлежащих основной линии тока. Соединив эти точки плавной кривой, получим линию тока.

Однако применять формулу (16) в приведенном виде не слишком удобно, так как трудно с удовлетворительной точностью откладывать углы при помощи транспортира, а даже малая неточность в построении угла приводит к тому, что не удается провести плавную кривую линии тока, соединяющую все найденные точки. Значительно упрощает дело использование декартовых координат. Связь декартовых и полярных координат точки определяется равенствами

(17)

Перед началом построения основной линии тока ответим на вопрос: в каком диапазоне нужно задавать значения полярного вектора? Основная линия тока включает в себя часть поверхности цилиндра, на которой т. е. . Длина полярного вектора при анализе внешнего обтекания цилиндра не может быть меньше его радиуса, поэтому, начиная по строение, следует задавать значения больше радиуса цилиндра ( или ), постепенно увеличивая их.

Возмущения, вносимые цилиндром в поток, затухают по мере удаления от него. На бесконечном удалении от цилиндра (как вверх, так и вниз по течению) линии тока выродятся в горизонтальные прямые.

Следует заметить, что вблизи поверхности цилиндра (малые r) точки должны располагаться несколько гуще, так как именно здесь линии тока имеют наибольшую кривизну. Для их построения необходимо рассчитать большое количество точек (т.е. задавать малый интервал между соседними значениями r). Вдали от поверхности цилиндра допустимо большее расстояние между соседними точками.

При определении расчетного шага между соседними значениям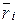и и можно поступать так: взять произвольный шаг 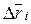, рассчитать две соседние точки линии тока, нанести их на чертеж и оценить, насколько они отстоят друг от друга. Если расстояние между точками велико, нужно уменьшить шаг 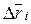. Целесообразные значения расчетного шага зависят от сочетания исходных данных и оказываются разными для всех трех линий тока, подлежащих построению. В качестве ориентира укажем, что приемлемый результат достигается, если число расчетных точек для каждой линии тока находится в пределах 15 – 20.

Сформулируем алгоритм построения основной линии тока по точкам.

1. На миллиметровую бумагу наносим декартову систему координат (ось абсцисс должна располагаться вдоль широкой стороны листа). Рисуем окружность радиуса R с центром в начале координат, если решено проводить построение в размерных координатах, или окружность единичного радиуса, если выбраны безразмерные координаты. Масштаб определяется из тех соображений, что при построении линий тока наиболее удаленные точки следует располагать на расстоянии 3–4 радиусов цилиндра по горизонтали от начала координат в обе стороны, то есть размер листа миллиметровки по горизонтали должен быть порядка 3–4 диаметров цилиндра. По вертикали достаточно 2–3 диаметров.

2. Отмечаем положение критических точек на поверхности цилиндра. Одна из критических точек получается при пересечении окружности радиуса R с лучом, исходящим из начала координат под критическим углом (в первом квадранте, если угол положительный, или в четвертом квадранте, если угол отрицательный); вторая критическая точка зеркально симметрична первой относительно оси ординат. Как уже отмечалось, построение углов при помощи транспортира весьма неточно; на чертеж удобнее наносить декартовы координаты критических точек, рассчитанные по формулам (17).

3. Задаем значения 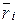. По формуле (16) определяем , затем находим и переходим к декартовым координатам.

4. Наносим точки на чертеж и при необходимости (если контур линии тока определен рассчитанными точками недостаточно подробно) вычисляем координаты дополнительных точек для промежуточных значений полярного радиуса.

5. Соединяем все построенные в выбранной координатной полуплоскости точки плавной кривой, начало которой – критическая точка на поверхности цилиндра. Наносим вторую половину линии тока симметрично первой относительно оси ординат.

Критерием качества расчетов является гладкость полученных кривых, если же рассчитанные точки не лежат на плавной кривой, при вычислениях, вероятно, допущены ошибки.

Дата добавления: 2015-08-20