Бюджетная линия

Если потребитель полностью расходует свой доход на товары Q1 Q2 то мы получаем равенство:

P₁Q₁+ P₂Q₂= R

Преобразовав данное равенство, получаем уравнение бюджетной линии, имеющее вид:

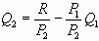
Бюджетная линия показывает набор комбинаций товаров Q1 и Q2, которые может приобрести потребитель, расходуя весь свой денежный доход. Наклон бюджетной линии определяется отношением P1/P2.

Кривая «доход-потребление» и кривая «цена-потребление»

С ростом реального дохода бюджетное ограничение сдвигается последовательно в положение В₁, В₂, В₃, …, В_n. Точки касания кривых безразличия с бюджетными ограничениями показывают последовательные положения равновесия потребителя в соответствии с ростом его дохода (рис.4.3).

Эта кривая, названная Дж. Хиксом «доход-потребление», в американской литературе получила название кривой уровня жизни. Если кривая «доход-потребление» - луч, выходящий из начала координат под углом 45°, это значит, что с ростом дохода потребитель в одинаковой пропорции увеличивает потребление и блага Х, и блага У. Если же покупки увеличиваются непропорционально, то изменяется угол наклона кривой.

Предположим в качестве постоянной величины доход потребителя, а в качестве переменной возьмем цену блага Х. Допустим, что цена блага Х снижается, т.е. Р¹_х > Р²_х > Р³_х > Р⁴_х и т.д.

Например, 1 единица блага Х стоила 100 $, а теперь стоит 50 $. Это значит, что за 100$ покупатель может купить 2 единицы блага Х. Графически это выглядит как сдвиг бюджетного ограничения из положения NX₁ в положение NX₂ (рис.4.4). Дальнейшее снижение цены соответственно отражают прямые NX₃, NX₅ и т.д. Соединив точки касания кривых безразличия с бюджетными ограничениями, мы получим кривую «цена-потребление».

Дата добавления: 2015-08-17