Задачи. МП-5 тема 2 примеры 7, 8, задачи 11, 12; ОЛ-3 примеры 19.200, 19.201.

Пример 7. Исследуется коэффициент упругости образцов резины. Для этого измерили его значения у 20 образцов 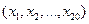. По техническим условиям требуется, чтобы разброс значений коэффициента около среднего не превышал 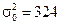. Рассмотрим 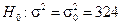, 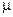− не известны. Важно обнаружить отклонение 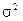от 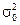в большую сторону, поэтому . Тогда 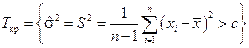, так как большие значения S ²свидетельствуют в пользу 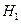. Удобнее, однако, вместо S ²воспользоваться пропорциональной ей статистикой 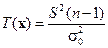, так как ее распределение при H ₀ известно и равно 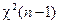. Ее большие значения также говорят в пользу Н ₁, т.е. 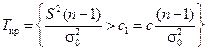. Зафиксировав некоторый размер критерия α, найдем c ₁ из условия 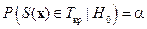. Имеем .

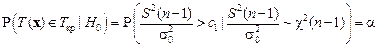Отсюда 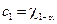, где 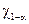− квантиль распределения 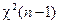уровня 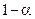. Если 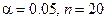, то 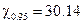. Пусть после проведения эксперимента получено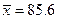

S ² = 538,2. Тогда вычисленное значение статистики 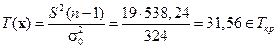. Гипотеза H ₀должна быть отвергнута.

Пример 8. При производстве некоторого лекарства X концентрация в нем вещества А должна в среднем равняться μ₀ = 2,4%. Дисперсия σ² известна и равна 0,0004%. (Вещество X токсично, в изменение его содержания даже в небольшое степени опасно для здоровья.) Измерено X у 25 проб (X ₁, Х ₂,..., X ₂₅) лекарства. Выдвинем гипотезы

H ₀: μ = μ₀, σ² = 0,0004

H ₁: μ ≠ μ₀, σ² = 0,0004

В силу того, что нас не устраивает отклонение от μ₀ как в большую, так и в меньшую сторону, критическая область является двусторонней: 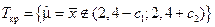. В статистике принято, что если T _кр состоит из двух интервалов, то каждый из них имеет одинаковую вероятность. Другими словами, 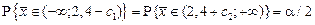, где α − размер критерия. Так как нормальное распределение симметрично относительно среднего μ( 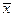имеет нормальное распределение при H ₀ с μ = μ₀), то из равенства этих двух вероятностей следует, что с ₁ = с ₂ = с.

Как и в предыдущем примере, удобнее взять вместо 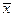статистику 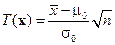(см. гипотезу а), которая при H ₀ имеет распределение N (0, 1). Тогда 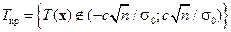. Определим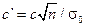

из условия 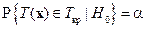, имеем

,

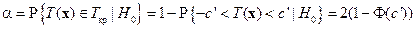где 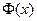− функция стандартного распределения. Отсюда 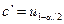− квантиль распределения N (0, 1) уровня 1 − α/2. Если α = 0,05, то 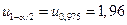. Следовательно, 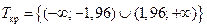. Если в результате эксперимента получено 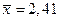(напомним, n = 25), то значение статистики 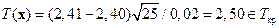. Гипотеза H ₀ должна быть отвергнута.

11. Проверку скорости полимеризации проводят на нескольких образцах полимеров. Предполагаемая скорость полимеризации составляет 24% /ч. В восьми опытах получены следующие результаты (%/ ч): 23,6; 22,8; 25,7; 24,8; 26,4; 24,3; 23,9; 25,0. Сделайте необходимые предположенияи проверьте утверждение, что результаты эксперимента не противоречат исходному предположению (α = 0,1).

12. Дисперсия предела прочности волокна на разрыв составляет 35,63 кг². Внесены изменения в технологический процесс, что может привести к стабилизации прочности (уменьшению дисперсии). Испытаны 15 образцов и получены следующие значения предела прочности: 151, 146, 161, 156, 160, 154, 147, 149, 162, 153, 160, 163, 155, 156, 149. Произошло ли уменьшение дисперсии (α = 0,1; 0,05)?

19.200. При подбрасывании монеты 10 раз герб выпал X раз. Классифицировать следующие гипотезы: H ⁽¹⁾: X имеет биномиальное распределение В (10, 1/2); H ⁽²⁾: X имеет биномиальное распределение В (10, p), причем 1/3 ≤ p ≤ 2/3; H ⁽³⁾: P{ X ≤ 3} > 1/2; H ⁽⁴⁾: монета не симметрична.

Ответ: Все гипотезы статистические; H ⁽¹⁾ и H ⁽⁴⁾ − простые, H ⁽²⁾ и H ⁽³⁾ − сложные гипотезы.

19.201. Считается, что новое антикоррозийное покрытие имеет эффективность 99%, если среди 20 испытанных образцов нет ни одного с признаками коррозии; в противном случае эффективность покрытия принимается равной 90%. Пусть p − вероятность появления признаков коррозии у одного образца. Предположим, что образцы обрабатываются и испытываются независимо один от другого. Рассмотрим нулевую гипотезу H ₀: p = 0,10 и альтернативную гипотезу Н ₁: p = 0,01. Ответить на следующие вопросы:

а) Какая статистика критерия используется в данной задаче, каковы ее распределение и область изменения?

б) Какова критическая область критерия?

в) В чем состоят ошибки первого и второго рода и чему равны их вероятности?

Ответ: а) Число образцов с признаками коррозии имеет биномиальное распределение B (20, p), V = {0, 1, 2,..., 20}; б) V_k = {0}; в) ошибка первого рода: принимается решение, что антикоррозийное покрытие имеет эффективность 99 %, в то время как его эффективность составляет 90%; ошибка второго рода: принимается решение, что антикоррозийное покрытие имеет эффективность 90%, в то время как его эффективность составляет 99%; α ≈ 0,122, β ≈ 0,182.

Дата добавления: 2015-08-20