Задачи. ОЛ-2 примеры 3.2, 3.4-3.8, МП-4 решение типовых примеров для задач 4-6 ДЗ, ОЛ-3 примеры 19.157

Пример 3.2. Рассмотрим построение приближенного до­верительного интервала для параметра p биномиального рас­пределения. Пусть проводилось n = 16 независимых испытаний с неизвестной вероятностью p „успеха" в каждом испытании, при этом наблюдалось k = 8 „успехов". Определим значения границ доверительного интервала для p с коэффициентом доверия γ = 0,9.

Значение точечной оценки параметра р определяется как

дисперсия этой оценки

Применяя приведенные выше формулы, получаем следующие значения для нижней и верхней границ доверительного интервала:

,

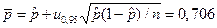
Пример 3.4. При помощи вольтметра, точность которого характеризуется средним квадратичным отклонением 0,2 В, проведено 10 измерений напряжения бортовой батареи. Найдем доверительный интервал для истинного значения напряжения батареи с коэффициентом доверия γ = 0,95, если среднее арифметическое результатов наблюдений = 50,2 В. Контролируемый признак имеет нормальный закон распределения.

Для нахождения доверительного интервала

где − квантиль нормального распределения уровня 1 −α/2, а α = 1 − γ. обратимся к таблице квантилей нормального распределения (см. табл.). По таблице находим

Поскольку

доверительный интервал имеет вид (50,2 − 0,1; 50,2 + 0,1), или (50,1; 50,3).

Пример 3.5. Из большой партии электроламп было отобрано случайным образом 400 шт. для определения средней про­должительности горения. Выборочная средняя продолжительность горения ламп оказалась равной 1220 ч. Найдем с коэффициентом доверия γ= 0,997 доверительный интервал для средней продолжительности горения электролампы по всей партии, если среднее квадратичное отклонение продолжительности горения равно 35 ч.

Независимо от закона распределения генеральной совокупности X (продолжительности горения электролампы) статистика

где

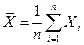
имеет асимптотически нормальное распределение с параметрами (0, 1), что следует из центральной предельной теоремы.

Поскольку объем выборки большой (n = 400), то границы доверительного интервала находим так же, как и в примере 3.4.

Для α = 1 − γ = 0,0028 находим квантиль нормального рас­пределения 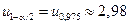. В силу соотношений

доверительный интервал имеет вид (1220 − 5,52; 1220 + 5,52), или (1214,48; 1225,52).

Пример 3.6. В результате пусков 10 ракет получены (в условных единицах) значения боковых отклонений точек попадания от точек прицеливания (см. табл.).

Номер ракеты
Отклонение	1,0	2,0	1,0	−0,1	−0,5	5,0	−1,0	3,0	0,5	1,0

Полагал, что случайная величина X (случайное боковое отклонение точек попадания от точек прицеливания) имеет нормальное распределение, построим доверительный интервал для ее математического ожидания с коэффициентом доверия γ = 0,99.

Для нахождения доверительного интервала воспользуемся статистикой

которая имеет распределение Стьюдента с n − 1 степенью свободы. Выборочное среднее имеет значение , а выборочная дисперсия − значение

Значение выборочного среднего квадратичного отклонения равно . По таблице квантилей распределения Стьюдента для п − 1 = 9 находим квантиль уровня . По условию задачи α = 1 − γ = 0,01

Следовательно, 1. Вычислив

получаем доверительный интервал (1,01 − 1,79; 1,01 + 1,79), или (−0,78; 2,80).

Пример 3.7. Из партии однотипных высокоомных сопротивлений отобрано 10 штук. У каждого из них измерены отклонения сопротивления от номинального значения (см. табл.).

Номер изделия
Отклонение			−2						−2

Предполагая, что контролируемый признак имеет нормальный закон распределения, найдем выборочное среднее , исправленную выборочную дисперсию S ²и доверительный интервал для дисперсии с коэффициентом доверия γ = 0,96.

Находим выборочное среднее 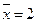и исправленную выборочную дисперсию S ² ≈ 5,88.

Чтобы построить доверительный интервал для дисперсии, вос­пользуемся статистикой

имеющей распределение χ²с n − 1 степенью свободы. По таблице квантилей распределения χ²(см. табл.) находим квантили и уровней и . В данном случае α = 1 − γ = 0,04 и распределение имеет девять степеней свободы. Следовательно,

; .

Для границ доверительного интервала получаем

;

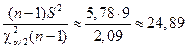
Отсюда находим доверительный интервал для дисперсии с коэффициентом доверия 0,96: (2,4; 24,9).

Пример 3.8. Найдем доверительный интервал для вероятности попадания снаряда в цель с коэффициентом доверия γ = 0,9, если после 220 выстрелов в цель попало 75 снарядов.

Используя таблицу квантилей нормального распределения (см. табл.), находим квантиль для α = 1 − γ. Поскольку α = 1 − γ = 0,1, то . Границы доверительного интервала имеют вид

,

Значит, доверительный интервал для вероятности попадания снаряда в цель следующий: (0,289, 0,393).

19.157. Найти 90% и 99%-ные доверительные интервалы для математического ожидания (среднего) следующих характеристик: емкость конденсатора, если = 20 мкФ, n = 16, среднеквадратичное отклонение известно и равно 4 мкФ.

Ответ: (18,35; 21,64), (17,42; 22,58).

Домашнее задание. ОЛ-2 задачи 3.13, 3.14, 3.16, 3.17, 3.19; МП-4 задачи 4-6 ДЗ, ОЛ-3 задачи 19.158

3.13. Постоянная величина измерена 25 раз с помощью прибора, систематическая ошибка которого равна нулю, а случайные ошибки измерения распределены по нормальному закону со средним квадратичным отклонением σ = 10 м. Определите значения границ доверительного интервала для измеряемой величины при коэффициенте доверия 0,99, если = 100 м.

Ответ: значение нижней границы 94,9 м, верхней − 105,1 м.

3.14. Оценка измеряемой величины определяется формулой

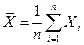
Результаты отдельных измерений не содержат систематической ошибки и подчинены нормальному закону распределения со средним квадратичным отклонением σ = 2,1. Определите интервальные оценки J_n с доверительной вероятностью 0,9 для значения измеряемой величины при различных объемах случайной выборки Х: а) n = 5, б) n = 10, в) n = 25.

Ответ: а) ( − 1,55; + 1,55); б) ( − 1,09; + 1,09); в) ( −0,69; + 0,69).

3.16. На основании 100 опытов было определено, что в среднем для производства детали требуется = 5,5 c, a = 1,7с. Сделав допущение, что время для производства детали распределено по нормальному закону, определите доверительный интервал для математического ожидания производства детали с коэффициентом доверия 0,85. Ответ: (5,25; 5,75).

3.17. По результатам измерений 100 резисторов, случайно отобранных из большой партии однотипных изделий, получена оценка сопротивления = 10 кОм. Найдите:

а) вероятность того, что для резисторов всей партии значения сопротивления лежат в пределах () кОм (среднее квадратичное отклонение измерения известно: σ = 1 кОм);

б) количество измерений, при котором с вероятностью 0,95 можно утверждать, что для всей партии резисторов значения сопротивления лежат в пределах (10 ± 0,1) кОм.

Ответ: а) 0,68; б) n ≥ 385.

3.19. На контрольных испытаниях 16 осветительных ламп были определены значения оценок математического ожидания и среднего квадратичного отклонения их срока службы, которые оказались равными = 3000 ч и = 20 ч соответственно. Считая, что контролируемый признак (срок службы лампы) имеет нормальный закон распределения, определите:

а) доверительный интервал для математического ожидания при доверительной вероятности 0,9;

б) вероятность, с которой можно утверждать, что абсолютная величина ошибки определения m не превысит 10 ч.

Ответ: а) (2991,2; 3008,8); б) 0,93.

19.158. Найти 90% и 99%-ные доверительные интервалы для математического ожидания (среднего) следующих характеристик: время безотказной работы электронной лампы, если = 500 ч, n = 100, среднеквадратичное отклонение известно и равно 10 ч.

Ответ: (498,35; 501,64), (497,42; 502,58).

Дата добавления: 2015-08-20