Постановка задачи. Задача состоит в определении высоты подъема центра шарика от всплывания при

Задача состоит в определении высоты подъема центра шарика от всплывания при деформировании металлической поверхности.

1) это не простая геометрическая задача;

2) проще всего ее определить экспериментально, замерив вертикальную координату точек и

; (4.5)

3) более просто, но приближенно величину подъема шара 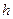можно определить, замерив, горизонтальный путь подъема и определив угол подъема 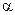из соотношения

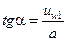; (4.6)

4) тогда высота подъема будет равна

; (4.7)

5) глубину вдавливания можно выразить через диаметр отпечатка

,

или

, (4.8)

Рис. 4.2 – Схема геометрии сдвига шарика

4.1.5. Приближенный сдвиговой закон пластического течения:

–поверхности металла жестким шариком (без ограничения всплыванию шарика)

1) в 4.1.2 показано, что для тонкого слоя приближенно закон течения жидкости записать в виде

, (4.9)

отсюда имеем динамическую вязкость

, (4.10)

2) при известных значениях 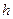[мм],

, ,

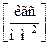размерность динамической вязкости

,

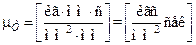3) кинематическая вязкость

.

Дата добавления: 2015-08-20