Дисперсия случайной величины. Среднее квадратичное отклонение

Для общего представления о распределении случайной величины важно знание не только ее математического ожидания, но и разброса возможных ее значений. Типичный пример представляет собой распределение случайных ошибок измерения.

В теории вероятностей для измерения разброса значений случайной величины около среднего значения используют понятие дисперсии.

Определение. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

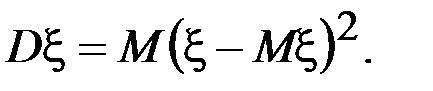(6.8)

Из определения ясно, что дисперсия является неотрицательной величиной и обращается в нуль, если случайная величина постоянна, т. е

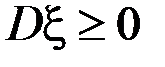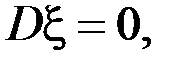и если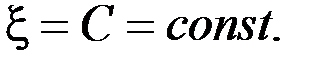

Дисперсии можно придать другую, более удобную форму. Для этого преобразуем формулу (6. 6) следующим образом:

Итак,

(6.9)

Из формулы (6.9) следует, что математическое ожидание квадрата случайной величины не меньше квадрата ее математического ожидания:

Определение. Величина называется средним квадратичным отклонением случайной величины , или стандартом.

Пример. Плотность распределения вероятностей случайной величины задается выражением

Найти математическое ожидание случайной величины , ее дисперсию и среднее квадратичное отклонение .

Решение. В данной задаче – непрерывная случайная величина. Ее числовые характеристики определяются по формулам:

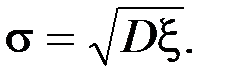
Вычисляем

как интеграл от нечетной функции по симметричному промежутку.

Тогда

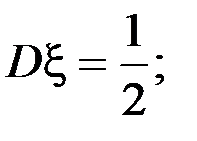
Дисперсию можно было вычислить по формуле

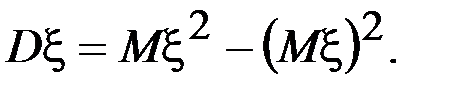
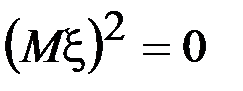Так как в данном случае , то и

Литература

1. Королев В.Т., Ловцов Д.А., Радионов В.В. Учебно-методический комплекс. Информационные технологии в юридической деятельности – М.: РАП, 2013.

2. Королев В.Т., Ловцов Д.А., Радионов В.В. Информационные технологии в юридической деятельности / Под ред. Д.А. Ловцова. – М.: РАП, 2011.

3. Королев В. Т. Информационные технологии в юридической деятельности. Учебно-методические материалы для практических занятий. - М.: РАП, 2012. (имеется в классе персональных компьютеров и на сайте академии).

4. Королев В.Т., Ловцов Д.А., Радионов В.В. Информационные технологии в юридической деятельности / Под ред. Д.А. Ловцова. – М.: РАП, 2011.

5. А.В. Могилев, Н.И. Пак, Е.К. Хеннер. Информатика. / Под ред. А.В. Могилева. М., Издательский центр «Академия». Изд. 1, 2006 г., 327 с..

6. Теория вероятностей и элементы математической статистики: учебное пособие / В. М. Радыгин. – 2-е изд. – Орел: Академия ФСО России, 2009. – 154 с.

Тема 7. Обработка числовой информации средствами информаци­онных технологий.

В рамках этой темы рассматриваются следующие вопросы:

Общая характеристика Excel. Разработка простейшей таблицы. Простейшие формулы в Excel. Работа с мастером функций. Диаграммы в Excel.Технология разработки комплексных документов. Базы данных в Excel.

Дата добавления: 2015-08-20