Математическое ожидание случайной величины

1. Пусть 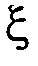– дискретная случайная величина, возможные значения которой принимаются соответственно с вероятностями 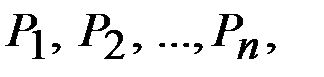так что .

Определение. Математическим ожиданием дискретной случайной величины называется число , определяемое
равенством

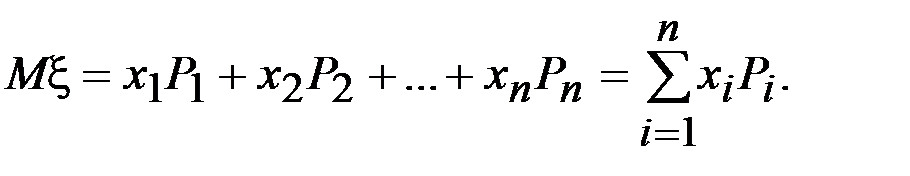(6.5)

Число возможных значений дискретной случайной величины может оказаться и бесконечным. В таком случае сумма вероятностей представляет собой ряд (сходящийся к единице). Для определения математического ожидания необходимо воспользоваться рядом

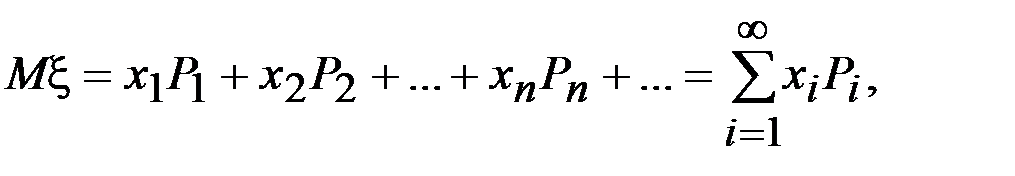(6.6)

причем для существования математического ожидания следует предположить, что ряд (6.2) абсолютно сходится.

Таким образом, математическим ожиданием, или средним значением дискретной случайной величины , называется сумма произведений всех ее возможных значений на соответствующие вероятности.

Определение. Математическим ожиданием непрерывной случайной величины 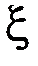называется интеграл

(6.7)

где – плотность распределения вероятностей в предположении, что данный интеграл абсолютно сходится.

Вычислим теперь математическое ожидание некоторых дискретных и непрерывных распределений случайных величин.

1) Пусть случайная величина имеет биномиальное распределение.

Это значит, что 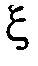принимает значения 0, 1, 2, …, n, а вероятности этих значений находятся по формуле Бернулли:

По определению математического ожидания находим

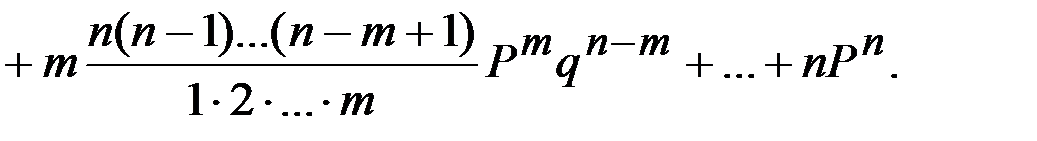
Вынося за скобку и производя сокращения, получаем

Выражение, стоящее в скобках, представляет собой разложение бинома и равно единице, так как . Поэтому получаем

.

Рассмотрим непрерывную случайную величину, подчиняющуюся закону равномерного распределения вероятностей. Плотность распределения вероятностей в этом случае имеет вид

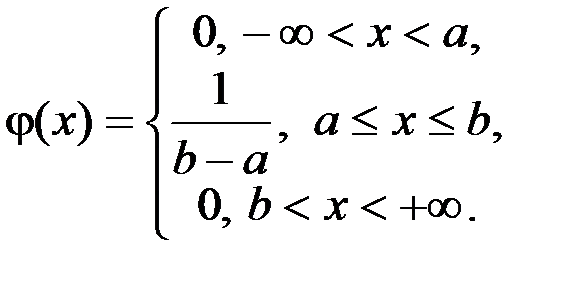
Используя формулу (3.4) для математического ожидания,
имеем

.

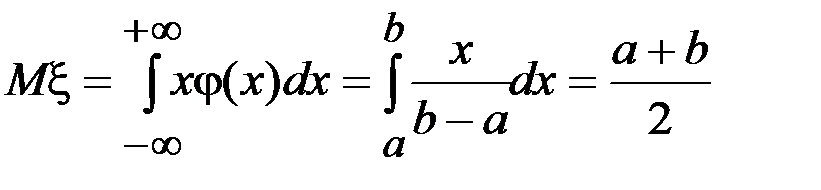Это означает, что математическое ожидание случайной величины , равномерно распределенной на отрезке , находится в центре этого отрезка.

4) Пусть непрерывная случайная величина 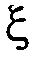имеет показательное распределение. Плотность распределения вероятностей в этом случае будет иметь вид

где 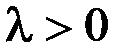– параметр.

Согласно формуле (6.4) для математического ожидания, получим

.

Интегрируя по частям интеграл , будем иметь

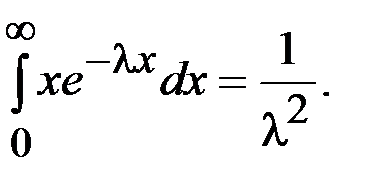
Тогда

Дата добавления: 2015-08-20