Многокритериальная оптимизация

Для задачи предыдущего задания найти решение при двух дополнительных критериях оптимизации. Для этого смоделировать следующие условия.

Затраты на износ оборудования при сдаче развлекательного павильона равны Wр тыс. руб., при сдаче торгового павильона Wт тыс. руб., при сдаче офисного павильона Wо тыс.

руб.

Рост репутации фирмы при сдаче развлекательного павильона равен Hр баллов, при сдаче торгового павильона Hт баллов, при сдаче офисного павильона Hо баллов.

Рассмотреть вариант оптимизации трех критериев: максимизации прибыли (как и было ранее в задании 2); минимизации износа оборудования; максимизации роста репутации

фирмы.

1. Определить оптимальные планы и значения критериев при оптимизации по каждому из них.

2. Определить оптимальный план методом свертки (взвешивания критериев). Вес первого критерия положить равным 5, второго 3, третьего 2. При взвешивании провести операцию обезразмеривания, поделив значения целевых функций на их максимальный коэффициент. Оценить значения критериев при таком подходе. Насколько они далеки от оптимальных при соответствующей однокритериальной

оптимизации?

3. Определить оптимальный план методом последовательных уступок. Уступка по первому критерию может составлять не более 20%, по второму – не более 35%. Оценить значения критериев при таком подходе. Как они отличаются от значений, определенных другими способами?

Во всех случаях записать четкий ответ, представляющий собой развернутое управленческое решение для поставленной экономической проблемы.

Wр	Wт	Wо	Hр	Hт	Hо

Решение:

Составим экономико-математическую модель задачи. Для этого обозначим 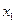– количество развлекательные павильонов, 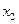– количество торговых павильонов, – количество офисных павильонов. Эта задача является задачей оптимального использования сырья, поэтому система ограничений имеет вид:

(1)

. (2)

Целевые функции равны:

(3)

Будем оформлять все вычисления в таблице Excel:

1) Оптимальный план задачи по критерию максимальной прибыли мы уже нашли в 1-ой задаче.

Для достижения максимальной прибыли 3550 млн. руб. в год требуется сдать в аренду 350 помещений под развлекательные павильоны и 220 помещений под торговые павильоны. При этом затраты составят 425000 тыс. руб., а репутация – 4250 балов.

Найдем оптимальный план задачи по критерию минимизации затрат на износ техники.

.

.

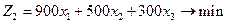Найдем решения этой задачи с помощью сервиса Excel Поиск решения.

Для запуска вычислений нажимаем кнопку «Выполнить». Получаем результат.

,

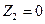Для достижения минимальных затрат на износ техники 0 тыс. руб. требуется сдать в аренду 0 развлекательных павильонов, 0 торговых павильонов и 0 офисных павильонов. При этом прибыль составит 0 млн. руб., а репутация – 0 балов.

Найдем оптимальный план задачи по критерию максимизации роста репутации фирмы.

.

.

Найдем решения этой задачи с помощью сервиса Excel Поиск решения.

Для запуска вычислений нажимаем кнопку «Выполнить». Получаем результат.

,

Для достижения максимального роста репутации 4250 балов требуется сдать в аренду 350 развлекательных павильонов и 220 торговых павильонов. При этом прибыль составит 3550 тыс. руб., а затраты составят 425000 тыс. руб.

2) Решим задачу методом свертки.

Проведем операцию обезразмеривания, поделив значения целевых функций на их максимальный коэффициент. Вес первого критерия положим равным 5, второго – 3, третьего – 2. Тогда получим целевую функцию.

Получим задачу линейного программирования:

Найдем решения этой задачи с помощью сервиса Excel Поиск решения.

Для запуска вычислений нажимаем кнопку «Выполнить». Получаем результат.

,

Выводы:

Для достижения максимума функции 2063,49 требуется сдать в аренду 350 развлекательных павильонов и 220 торговых павильонов.

3) Решим задачу методом последовательных уступок. Воспользуемся средствами Microsoft Excel.

Вначале решаем задачу для функции прибыли Z₁.

Получим ,

На втором этапе оптимизируется вторая целевая функция. При этом первую, в соответствие с методом последовательных уступок, можно ухудшить величину не более чем 20%. По этой причине, на втором шаге, функция прибыли может быть не меньшее, чем 3550·0,8 = 2840. Вызываем надстройку «Сервис/Поиск решения», теперь найдем минимум функции затрат, при этом, добавим ограничение для функции прибыли Z₁ ≥ 2840.

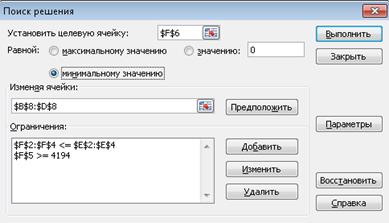
Получим ,

На третьем этапе делаем уступку по второму критерию. Величина уступки не должна превышать 35%. Так, как вторая функция минимизируется, то ее значение не должно превышать 307571*1,35 = 415221,4. Вызываем надстройку «Сервис/Поиск решения», теперь найдем максимум функции репутации, при этом, добавим ограничение для функции прибыли Z₂ ≤ 415221,4.

Получим окончательное решение:

,

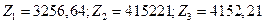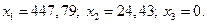
Выводы:

Для достижения максимальной прибыли 3256,64 млн. руб. в год, минимальных затрат на износ 415221 тыс. руб. и максимального роста репутации 4152,21 балов требуется сдать в аренду 447,79 развлекательных павильонов и 24,43 торговых павильонов.

Дата добавления: 2015-08-20