Оптимизация использования ограниченных ресурсов

Арендодатель имеет возможность сдавать помещения под развлекательные, торговые и офисные павильоны. Развлекательный павильон занимает S_р десятков квадратных метров

площади, требует E_р КВатт энергии и R_р человек обслуживающего персонала. Торговый павильон занимает S_т десятков квадратных метров площади, требует E_т КВатт энергии и R_т человек обслуживающего персонала. Офисный павильон занимает S_o десятков квадратных метров площади, требует E_o КВатт энергии и R_o человек обслуживающего персонала. Прибыль с одного развлекательного павильона равна P_р миллионов рублей в год, прибыль с одного торгового павильона равна P_т млн. руб. в год, прибыль с одного офисного павильона равна P_о млн. руб. в год. Общие площади, сдаваемые в аренду, равны S_общ десятков квадратных метров, максимальная мощность энергетической подстанции равна E_общ КВатт, штат обслуживающего персонала равен R_общ человек.

Цель: определить оптимальный с точки зрения получения прибыли план сдачи помещений в аренду (количество развлекательных, торговых и офисных павильонов).

1) Составить экономико-математическую модель задачи.

2) Найти оптимальное решение. Дать экономическую интерпретацию полученного решения. Сформулировать оптимальное управленческое решение в описанных условиях.

3) Определить интервалы устойчивости полученного плана при изменении коэффициентов целевой функции. Сделать выводы об устойчивости полученного плана к изменению рыночных цен (прибыли от единицы площади каждого вида).

4) Определить двойственные оценки ресурсов. Дать экономическую интерпретацию двойственных оценок. Определить интервалы устойчивости двойственных оценок при изменении каждого ресурса по отдельности. Сделать выводы о рентабельности приобретения дополнительных ресурсов и их количества.

5) Записать четкий ответ для поставленной экономической проблемы.

Sp

Eр

Rp

Sт

Eт

Rт

So

Eo

Ro

Pp

Pт

Po

Sобщ

Eобщ

Rобщ

Решение:

1) Составим экономико-математическую модель задачи. Для этого обозначим 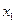– количество развлекательные павильонов, 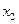– количество торговых павильонов, – количество офисных павильонов. Эта задача является задачей оптимального использования сырья, поэтому система ограничений имеет вид:

(1)

где справа стоит количество каждого вида сырья, которое не может быть превышено в процессе производства изделий. Эти ограничения являются нетривиальными.

Далее, количество изделий физически является неотрицательными (нельзя произвести отрицательное количество изделия), что дает нам тривиальные ограничения задачи:

. (2)

Наконец, функция цели (целевая функция) представляет собой общую стоимость построенных зданий, и эта функция в данной задаче оптимизируется на максимум:

(3)

1) Найдем решения этой задачи с помощью сервиса Excel Поиск решения.

Открываем электронную книгу Excel и, как и для решения однокритериальной задачи определяем ячейки под переменные x ₁, x ₂, x ₃.

Вызываем надстройку «Поиск решения» в меню «Сервис». Оптимизируем целевую функцию.

После открытия окна «Поиск решения» в поле «Установить целевую» ставим курсор и делаем ссылку на ячейку F5, щелкая по ней мышью. В окне появится $F$5. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Равной максимальному значению».

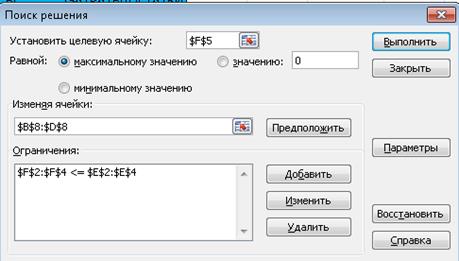
Для запуска вычислений нажимаем кнопку «Выполнить». Получаем результат.

,

Для достижения максимальной прибыли 3550 млн. руб. в год требуется сдать в аренду 350 помещений под развлекательные павильоны и 220 помещений под торговые павильоны.

2) В процессе поиска оптимального решения MS-Excel формирует так называемый отчет об устойчивости, в котором, в частности, выдает интервал изменений коэффициентов целевой функции, внутри которого их изменение не приводит к изменению oоптимального решения. Для получения этого отчета, после того как "Поиск решения" нашел оптимальное решение, нужно в окне "Результаты поиска решения", перед тем как нажать на кнопку Ok, щелкнуть мышкой по строке "Устойчивость" в списке "Тип отчета". Тогда после нажатия на кнопку Ok MS-Excel создаст дополнительный лист "Отчет об устойчивости".

Microsoft Excel 12.0 Отчет по устойчивости
Рабочий лист: [3 задача ВАР 7.xlsx]Лист1
Отчет создан: 24.03.2013 16:15:17
Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
	$B$8	ПЛАН T1
	$C$8	ПЛАН T2					1,5
	$D$8	ПЛАН T3		-3			1E+30
Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
	$F$2	P1 ЗАТРАТЫ				1E+30
	$F$3	P2 ЗАТРАТЫ		0,6		254,5454545
	$F$4	P3 ЗАТРАТЫ

Первая таблица отчета об устойчивости "Изменяемые ячейки" содержит столбцы "Целевой коэффициент", "Допустимое увеличение" и "Допустимое уменьшение". В первом из них даны исходные значения целевых коэффициентов: прибыль от сдачи в аренду (7 млн. руб. в год) торговых павильонов (5 млн. руб. в год) и офисных павильонов (3 млн. руб. в год). Второй и третий столбцы содержат информацию об интервале устойчивости найденногооптимального решения. При увеличении прибыли от сдачи в аренду развлекательных павильонов до 10 млн. руб. в год (на 3 млн. руб. в год больше исходного значения) и при се уменьшении до 5 млн. руб. в год оптимальное решение не изменя­ется. Аналогично второй целевой коэффициент может изменять­ся в пределах от 3,5 млн. руб. в год (уменьшение на 1,5 млн. руб. в год относительно исходного значения) до 7 млн. руб. в год и третий целевой коэффициент может изменять­ся в пределах от -∞ до 6 млн. руб. в год.

3) Двойственная задача и её решение.

Рассмотрим исходную задачу. При переходе к двойственной задаче нужно выполнить ряд правил. Во-первых, каждому ограничению исходной задачи соответствует переменная двойственной задачи. Таким образом, здесь будут три двойственные переменные 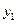, , 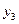. Во-вторых, ограничения двойственной задачи соответствуют столбцам системы; неравенства типа превращаются в неравенства типа 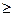, а свободными членами становятся коэффициенты при соответствующих переменных целевой функции. В-третьих, целевая функция двойственной задачи оптимизируются не на максимум, а на минимум; коэффициентами становятся свободные члены системы. Наконец, двойственные переменные , как и переменные задачи, подчиняются тривиальным условиям неотрицательности. С учетом этих замечаний задача, двойственная задаче, имеет вид:

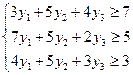
Решение двойственной задачи можно получить из "Отчета об устойчивости".

Теневые цены - это оценки y_i двойственной задачи.

Таким образом, , , .

Пределы изменения b_i, в которых оптимальное решение соот­ветствует той же самой угловой точке, также даны в таблице "Ог­раничения" ("Допустимое увеличение" и "Допустимое умень­шение"). Получаем интервалы устойчивости двойственных оценок по отношению к изменению ресурса каждого вида

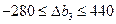
4) Выводы:

Для достижения максимальной прибыли 3550 млн. руб. в год требуется сдать в аренду 350 помещений под развлекательные павильоны и 220 помещений под торговые павильоны.

При увеличении прибыли от сдачи в аренду развлекательных павильонов до 10 млн. руб. в год и при ее уменьшении до 5 млн. руб. оптимальное решение не изменя­ется. Прибыль от сдачи в аренду торговых павильонов может изменяться в пределах от 3,5 до 7 млн. руб. в год и прибыль от сдачи в аренду офисных павильонов может изменять­ся в пределах от -∞ до 6 млн. руб. в год.

Интервалы устойчивости двойственных оценок по отношению к изменению ресурса каждого вида:

Для площади: ;

Для энергии:

Для обслуживающего персонала: .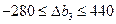

---

Дата добавления: 2015-08-20