Гипотеза вейлевской кривизны (ГВК).

Гипотеза вейлевской кривизны (ГВК). Насколько я понял позицию Стивена, я не думаю, что наши разногласия в этом вопросе очень велики. Для начальной сингулярности кривизна Вейля приблизительно равна нулю, а для конечной — очень велика. Стивен утверждает, что в начальном состоянии должны были существовать малые квантовые флуктуации, указывающие на то, что гипотеза, по которой начальная

Твисторный взгляд на пространство-время · 121

вейлевская кривизна должна быть точно равна нулю, неприемлема. Я не думаю, что в этом вопросе у нас действительно разногласия. Утверждение о том, что кривизна Вейля в точности равна нулю, является классическим, поэтому определенно существует некоторый произвол в точной формулировке гипотезы. Малые возмущения в квантовом режиме, с моей точки зрения, определенно должны быть учтены. Нам действительно необходимо что-то, чтобы заставить вейлевскую кривизну быть близкой к нулю. Можно также ожидать тепловых флуктуаций в тензоре Риччи (благодаря вкладу материи) в ранней Вселенной, и возможно, что в конечном счете это приведет, вследствие нестабильности Джинса, к образованию черных дыр общей массой порядка 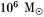. Тогда близость сингулярностей в этих черных дырах приведет к большому значению вейлевской кривизны, но это будут сингулярности не начального, а скорее конечного типа, что согласуется с ГВК.

Я согласен со Стивеном, что ГВК является «ботанической», т.е. гипотезой на уровне феноменологии, а не понимания. Необходима более глубокая теория, чтобы объяснить ее. Возможно, что «предположение об отсутствии границ» (ПОГ) Хартля и Хокинга является хорошим кандидатом на структуру начального состояния. Однако мне кажется, что для объяснения конечного состояния нам необходимо что-то совсем другое. В частности, теория, которая объясняет структуру сингулярностей, должна нарушать Т, РТ, СТ и СРТ инвариантности для того, чтобы могло возникнуть что-то, удовлетворяющее ГВК. Это нарушение временной симметрии может быть весьма малым: оно могло бы неявно содержаться в правилах той теории, которая находится за рамками квантовой механики (КМ). Стивен утверждал, что с учетом хорошо известной теоремы квантовой теории поля (КТП) можно ожидать, что теория будет СРТ-инвариантна. Однако доказательство этой теоремы подразумевает, что выполняются обычные правила КТП, и что фоновое пространство является плоским. Я думаю, что и Стивен, и я согласны, что второе условие не выполняется, хотя я считаю, что и первое тоже нарушается.

Мне также кажется, что та точка зрения, которую Стивен предложил относительно ПОГ, не приводит к отсутствию

122 · Глава 6 — Роджер Пенроуз

белых дыр. Если я понял точку зрения Стивена правильно, то ПОГ приводит к существованию двух решений: одно (А) соответствует случаю, когда возмущения увеличиваются при удалении от сингулярности, в то время как в другом (Б) они затухают. Случай (А) связан по существу с Большим взрывом, а (Б) описывает сингулярности черных дыр и Большого хлопка. Стрела времени, определяемая вторым законом термодинамики, задает направление от решения (А) в решение (Б). Однако я не вижу, как эта интерпретация ПОГ исключает белые дыры, соответствующие (Б)-типу. Отдельно у меня вызывает сомнения «процедура евклидизации». Аргументы Стивена основаны на факте, что можно склеить вместе евклидово и лоренцовское решение. Однако существует только несколько пространств, в которых это можно сделать, поскольку требуется, чтобы они имели как евклидов, так и лоренцовский сектор. Общий случай определенно очень далек от этого.

Дата добавления: 2015-08-20