Два естественных выбора для интеграла по путям в квантовой гравитации

1. Асимптотически евклидовы метрики.

2. Компактные метрики без границ.

Первый класс асимптотически евклидовых метрик, очевидно, подходит для расчетов процессов рассеяния (рис. 5.1). В них можно рассматривать частицы, приходящие из бесконечности и снова уходящие на бесконечность. Все измерения проводятся на бесконечности, где имеется плоская фоновая метрика, и можно обычным образом интерпретировать малые флуктуации полей как частицы. При этом не стоит спрашивать, что же происходит в области взаимодействия посередине. Именно поэтому в интеграл по путям входят все возможные истории в области взаимодействия, а тем самым и все асимптотически евклидовы метрики.

Однако в космологии представляют интерес измерения, которые выполняются не на бесконечности, а в конечной области. Мы находимся внутри Вселенной, а не смотрим на нее снаружи. Чтобы увидеть, в чем здесь разница, сначала предпо-

92 · Глава 5 — Стивен Хокинг

Рис. 5.1. При расчетах рассеяния мы измеряем характеристики частиц, приходящих и уходящих на бесконечность.

Таким образом мы хотим изучать асимптотически евклидовы метрики

ложим, что интеграл по путям в космологии берется по всем асимптотически евклидовым метрикам. Тогда в вероятности измерений в конечной области будут вноситься два вклада. Первый получается от связных асимптотически евклидовых метрик, второй — от несвязных метрик, которые состоят из компактного пространства-времени, содержащего область измерений, и отдельной асимптотически евклидовой метрики (рис. 5.2). Такие несвязные метрики не могут быть исключены из интеграла по путям по той причине, что их можно приближенно заменить на связные метрики, в которых различные компоненты соединены вместе тонкими трубками или воронками, дающими пренебрежимо малый вклад в действие. Несвязные компактные области пространства-времени не могут влиять на вычисление результатов рассеяния, поскольку они не связаны с бесконечностью, где производятся все измерения. Но они будут влиять на космологические измерения, которые производятся в конечной области. Действительно, вклад от таких несвязных метрик будет доминировать над вкладом от связных асимптотически евклидовых метрик. Поэтому, даже если рассматривать интеграл по путям в космологии по всем асимптотически евклидовым метрикам, эффект

Квантовая космология · 93

Рис. 5.2. Космологические измерения выполняются в конечной области, так что мы можем рассмотреть два типа асимптотически евклидовых метрик: связные (сверху) и несвязные (снизу)

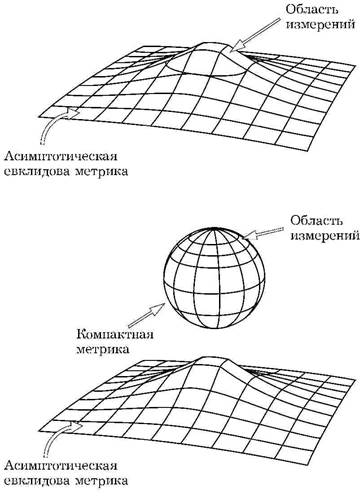
будет почти такой же, как если бы интеграл по путям вычислялся по всем компактным метрикам. Следовательно, кажется более естественным брать интеграл по путям в космологии по всем компактным метрикам без границ, как это было предложено Джимом Хартлем и мной в 1983 г. (Хартль и Хокинг, 1983).

Дата добавления: 2015-08-20