Читайте также:
|
Умножим почленно первое на 
, второе на 
и вычтем второе из первого:
- дифференциальная теорема Умова-Пойнтинга.
Проинтегрируем последнее по 
:
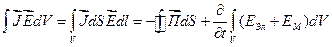, где 
, а 
,
- вектор Умова-Пойнтинга
Выведенные формулы 
и 
верны только тогда, когда материальные уравнения линейны. В общем случае это не так.
Теорема Умова-Пойнтинга в интегральной форме утверждает – чтобы получить энергию из заданного объёма, нужно обеспечить разряд конденсаторов или индуктивных накопителей.
Теорема Умова-Пойнтинга имеет громадное научно-техническое значение, поскольку доказывает материальность ЭМП.
27 нету
Дата добавления: 2015-08-20; просмотров: 127 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Продольные волны | | | Структура материи: частицы поля. Роль электромагнитных полей. |