Свойства, непосредственно получаемые из обычных правил дифференцирования

· Линейность:

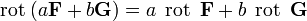
для любых векторных полей F и G и для любых постоянных чисел a и b.

· Если 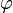— скалярное поле, а F — векторное, тогда:

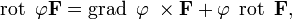
или

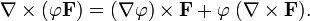
· Дивергенция ротора равна нулю:

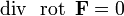или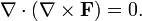

При этом верно и обратное: если поле F бездивергентно, оно вихрь некоторого поля G (векторного потенциала):

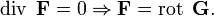
· Если поле F потенциально, его ротор равен нулю (поле F — безвихревое):

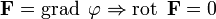
Верно и обратное: если поле безвихревое, то оно потенциально:

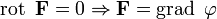
для некоторого скалярного поля 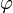(то есть найдется такое 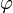, что F будет его градиентом).

· (Следствие из свойств выше): два (и сколько угодно) различных векторных поля могут иметь одинаковый ротор. При этом различаться они будут обязательно на безвихревое поле, то есть на градиент некоторого скалярного поля.

· Ротор ротора равен градиенту дивергенции минус лапласиан:

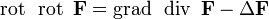
Дата добавления: 2015-08-20