Читайте также:
|
Все определения ротора, о которых будет говориться в данном параграфе полностью эквивалентны (по крайней мере для случая дифференцируемого векторного поля), и в качестве основного, в принципе, можно выбрать любое из них. Остальные тогда оказываются формулами, которые могут быть более удобны в том или ином случае.
Прежде всего, перечислим явно те варианты, которые уже упоминались в статье выше и могут при желании каждое играть роль определения ротора.
· Классическое определение, приведённое в данной статье как основное (см.Математическое определение).
· Вычислительная формула через производные компонент в декартовых координатах, приведённая там же.
· Формула в параграфе Физическая интерпретация.
Кроме них полезно упомянуть:
· Выражение через символ Леви-Чивиты, дающее наиболее компактную координатную запись, а во втором варианте - общую формулу для любых криволинейных координат (ограничиваясь[6], правда, только размерностью 3):
· В варианте для ортонормированного базиса (обычных декартовых координат):
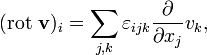
· В тензорной записи для произвольных (в том числе косоугольных и криволинейных координат; используя верхние и нижние индексы и правило суммирования Эйнштейна):
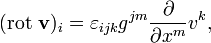
где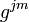 
- метрический тензор в представлении с верхними индексами. В последнем случае (общем) важно упомянуть, что под значком 
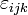имеется в виду именно тензор, включая множитель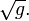 
· Интересную и довольно красивую форму определения, иногда используемую в литературе:
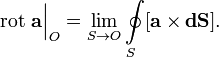
Дата добавления: 2015-08-20; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства, непосредственно получаемые из обычных правил дифференцирования | | | Общий случай |