Лабораторна робота №5

Функції

Зміст роботи: програмування з використанням функцій.

Функція формально задається описом типу результату, формальних параметрів и блоку, який задає виконувані дії функції.

Приклад:

double // тип результату

linfunc (double x, double y, double z)
// ім’я функції, список параметрів

{ // блок тіла функції

return (x*y+z); // значення, що повертається
// функцією

}

Оператор return може не повертати ніякого значення або повертає значення відповідного виразу. Функція, що не повертає ніякого значення повина бути описана, як та, що має тип void.

Є два способи виклику функції:

ім’я_функції (е1, е2,..., еN);

(*покажчик_на_функцію)(е1, е2,..., еN);

покажчик_на_функцію – це змінна, значенням якої є адреса функції. Адреса функції може бути присвоєна покажчику оператором

покажчик_на_функцію = ім’я_функції ;

Аргументи (фактичні параметри) передаються по значенню, тобто кожний вираз е1, е2, …, еN обчислюється і його значення передається функції. Якщо вхідне значення необхідне функції для деяких обчислень або дій, то фактичним аргументом повино бути ім’я змінної, а якщо функція буде змінювати значення змінних в програмі, що її визвала, то необхідно використовувати адреси змінних.

В першому завданні для значень одержіть таблицю значень функції 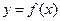. Таблиця повинна містити п’ять стовпців з заголовками:

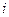
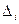
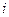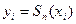Тут - номер аргументу , - номер ітеративного кроку, на якому перший раз виконалась умова , де - член ряду, - значення функції ( - частинна сума відповідного ряду, включаючи ), - похибка обчислень. Виконайте обчислення з точністю 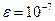та .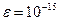

В другому завданні знайдіть рекурсивний і не рекурсивний розв’язок задачі. Дослідіть, для яких значень аргумента функції можливо отримати розв’язок за рекурсивною формулою.

Варіант 1.

1. ,

2. Обчисліть значення поліномів Чебишева 1-го роду: , , .

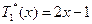Варіант 2.

1. ,

2. Одержіть ряд Фібоначчі і золотий перетин : , , ; .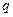

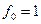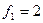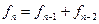Варіант 3.

1. ,

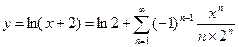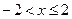
2. Обчисліть значення поліномів Ерміта: , ,

Варіант 4.

1. ,

2. Обчисліть коефіцієнти бінома Ньтона: , , .

Варіант 5.

1. ,

2. Обчисліть та .

Варіант 6.

1. ,

2. Підрахуйте кількість всіх розміщень із елементів по : , .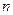

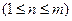Варіант 7.

1. ,

2. Одержіть всі перестановки символів a,b,c,d.

Варіант 8.

1. ,

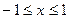
2. Обчисліть виконуючи тільки адитивні операції.

Варіант 9.

1. ,

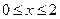
2. Обчисліть значення полінома в точці 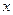за правилом Горнера.

Варіант 10.

1. ,

2. Обчисліть значення функцій Аккермана-Петера: , , .

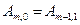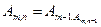Варіант 11.

1. ,

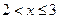
2. Обчисліть значення поліномів Лагера: , ,

.

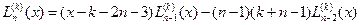Варіант 12.

1. ,

2. Розкладіть ціле число на його прості множники.

Варіант 13.

1. ,

2. Перетворіть послідовним додаванням або відніманням 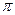аргумент 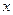до проміжку .

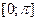Варіант 14.

1. ,

2. Обчисліть біноміальні коефіцієнти: , , .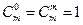

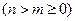Варіант 15.

1. ,

2. Обчисліть 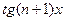, якщо відомо що , .

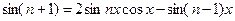Контрольні запитання до лабораторної роботи №5

1. Як визначити функцію?

2. Як передавати функції інформацію?

3. Де необхідно описувати аргументи?

4. Яка різниця між формальними і фактичними аргументами?

5. Де необхідно описувати локальні змінні функції?

6. Коли і як використовують оператор return?

7. Коли і як використовують адреси і покажчики для доступу до змінних?

8. Для чого служить і коли треба задавати прототип функції?

---

Дата добавления: 2015-08-20