Теория идеального ветряка проф. Г. X. Сабинина

Отличие этой теории от прежних теорий заключается в том, что при определении осевой силы давления потока на ветроколесо импульс сил подсчитывается по вихревому соленоиду в том месте, где он принял уже установив­шуюся цилиндрическую форму, а не в момент его образо­вания, как принималось прежними теориями. Так как соленоид в цилиндрической части имеет площадь сечения большую, чем площадь, ометаемая ветроколесом, то осевая сила и коэффициент использования энергии ветра, по теории Г.X. Сабинина, получаются несколько боль­шими.

Как следствие принятых условий для определения иде­ального ветряка получаем следующее: осевые ско­рости постоянны по всему сечению струи, что вытекает из вихревой теории гребного винта Н.Е. Жуковского: циркуляция по любому замкнутому контуру внутри ухо­дящей струи равна нулю, и, следовательно, поток не завихрен и тангенциальные скорости равны нулю. Циркуляция в плоскости вращения ветряка равна нулю, и есть только скачок давления. Концевые потери также равны нулю, так как они обратно пропорциональны числу лопастей и угловой скорости вращения.

Пусть равномерный поток, обладающий скоростью V, набегает на ветряк, как было показано на рис.1. Про­ведём через окружность, описываемую концами лопастей, линии тока, образующие бутылеобразную поверхность АА'ВВ'СС', которую назовём «ограничивающей поверх­ностью».

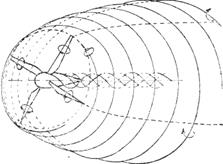
Рис. 2. Образование вихревого соле­ноида за ветроколесом скорости,

вызванные соленоидом, будут направлены в обратную сторону

по отношению к скорости потока.

По мере удаления от ветряка, ограничивающая по­верхность постепенно переходит в цилиндрическую по­верхность. Часть потока, заключённая внутри ограни­чивающей поверхности, называется рабочим потоком. Ограничивающая поверхность ВВ'СС', лежащая поза­ди ветряка, представляет собой поверхность раздела, образованную бесконечно тонким вихревым слоем, состоя­щим из ряда вихревых шнуров бесконечно малой интен­сивности, сходящих с концов лопастей и навитых в виде спирали с бесконечно малым шагом на поверхность раз­дела (рис. 2). Таким образом, поверх­ность раздела будет представлять собой вихревой соленоид. Вихревой слой соле­ноида можно себе схематически пред­ставить состоящим из ряда вихревых шнуров, диаметр ко­торых равен толщи­не вихревого слоя. Окружная скорость наружных частиц та­кого вихря близка к скорости прилегающего к нему не­ завихренного слоя. Скорости к центру вихря убывают, ибо мы можем представить, что вихрь вращается, как твёрдое тело.

Такой бесконечно тонкий, вихревой слой не требует на своё образование энергии так как его живая сила бесконечно мала вследствие бесконечно малой массы слоя, в то время как максимальные его скорости ко­нечны. Предполагая, что вихревой соленоид при достаточном удалении от ветряка принимает цилиндрическую форму и в таком виде уходит в бесконечность, получаем, что струи как внутри соленоида, так и вне его идут парал­лельно и давления во всех точках потока, достаточно удалённых от ветряка, постоянны.

Деформация потока, производимая идеальным ветря­ком, будет сводиться к наложению скоростей, вызывае­мых вихревым соленоидом на равномерный поток, причём приращение количества движения жидкости, произво­димое ветряком, будет равно количеству движения, вы­зываемого вновь образуемой цилиндрической частью соленоида.

На рис.3 приведена схема прохождения воздушного потока через ветроколесо. В сечении А – А', бесконечно далеко перед ветряком, поток имеет скорость V и поверхность S. В сечении В – В',в плоскости ветроколеса, осевая скорость потока равна V – v₁ где v₁ – скорость, вызываемая вихревым соленоидом на его конце; ометаемая поверхность – S₁. В сечении С – С', бесконечно далеко за ветряком, ско­рость в цилиндрической части соленоида составляет V – v₂, где v₂ — скорость, вызываемая соленоидом, в достаточном удалении от ветряка. Скорость потока вне цилиндрический части соленоида будет V, так как соле­ноид во внешнем потоке не вызывает никаких скоростей.

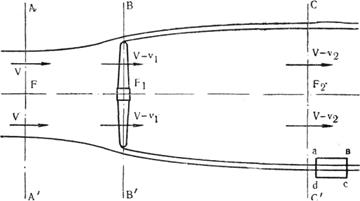
Рис. 3. Схема прохождения воздушного потока через ветроколесо.

Скорость движения самого бесконечно длинного вих­ревого соленоида относительно потока проф. Г.X. Са­бинин принимает равной половине скорости, вызванной соленоидом внутри его, именно равной v₂/2. Так как соле­ноид уносится потоком со скоростью V, то, следовательно, абсолютная его скорость будет – (V-v₂)/2; это будет ско­рость образования вихревого соленоида.

Определим циркуляцию скорости вихревого солено­ида на единицу его длины, для чего опишем прямоуголь­ный контур abcd так, чтобы его стороны ab и cd были па­раллельны оси струи, а стороны bс и da перпендикулярны к ней (рис. 3). Обходя контур по направлению часовой стрелки, имеем: циркуляция по стороне ab, будет ab (V – v₂),так как скорость V – v₂ параллельна ab. Циркуляция по cd будет cd×V; циркуляция по сторонам bс и da равна нулю, так как эти стороны перпендикулярны к скоростям V и V–v₂ цир­куляция же в том месте, где эти стороны пересекают вих­ревой соленоид, также равна нулю, так как вихревой слой бесконечно тонок, а окружная скорость вращения частиц вихревого слоя конечна. Циркуляция по всему контуру будет: ab×(V – v₂) – cd×V, так как ab = cd, то циркуляция по контуру abcd равна: – ab×v₂.

Циркуляция на единицу длины соленоида: (а)

Подсчитаем импульс силы, потребной для образования вихревого соленоида, для чего воспользуемся следующей теоремой. Импульс силы PDt, необходимый для образо­вания вихревого кольца, равен площади вихревого коль­ца S, умноженной на циркуляцию скорости Г вокруг вихря и умноженной на плотность жидкости r: PDt = rSГ. (б) Здесь импульс силы направлен по нормали к плоско­сти вихревого кольца.

Если разбить соленоид на элементарные кольца с про­тяжением по оси соленоида dz, то на единицу длины со­леноида придётся 1/dz вихревых колец.

Импульс силы для образования одного вихревого кольца соленоида составляет: rS₂ dГ, (в) где dГ – циркуляция скорости одного кольца; S ₂ – площадь сечения цилиндрической части со­леноида. Так как за время dt длина соленоида увеличивается на величину 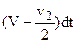, то за этот промежуток времени образуется число колец: 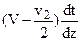(г)

Импульс силы на ветряк за время dt будет численно равен сумме импульсов, необходимых для образования вихревых колец, появившихся в то же время. Эта сумма на основании уравнений (в) и (г) составит: 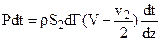(д). Перепишем это уравнение в таком виде: 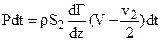(е), но 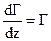– циркуляция скорости на единицу длины соленоида, которая, согласно уравнению (а), равна – v². Поэтому, сокращая уравнение (е) на dt и подставляя в него вместо Г его значение –v₂, получим: 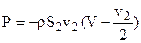Преобразуем это уравнение, представив его в виде двух слагаемых: (1)

Выражение, стоящее в квадратных скобках первого члена правой части уравнения, есть масса воздуха, про­ходящая через ометаемую площадь в единицу времени, а весь первый член, т.е. [pS₂(V–v₂)]v₂, есть прираще­ние количества движения этой массы, которую обозначим через m₁. Второй член по своей размерности есть то же приращение количества движения в единицу времени. Он не может быть разбит на два множителя так, чтобы одно­му множителю соответствовала определённая масса жид­кости, а другому некоторая скорость, одинаковая для всех частиц этой массы, так как нам пока неизвестен тот процесс, в котором происходит образование количества движения, имеющего выражение .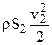

Для удобства дальнейших рассуждений умножим и разделим это выражение, т.е. второй член равенства (1), на v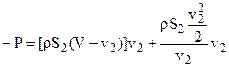₂: (2)

Дробь, стоящая в квадратных скобках, не может быть сокращена на v₂, так как числитель этой дроби по своей физической сущности представляет интеграл: 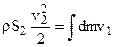, где закон образования функции m и v нам не известен. Выражение называется присоединённой массой 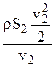и обозначается через m₂. Заметим, что rS₂(V – v₂) = m₁. После чего уравнение (2 70а) можно переписать так: – P = (m₁ + m₂)v₂ (3)

Сумма (m₁ + m₂)называется увлечённой мас­сой, а скорость v₂ называется скоростью вле­чения. Таким образом, уравнение (3 71) можно форму­лировать так: лобовое давление, произво­димое потоком на ветряк, будет рав­но произведению увлечённой массы на скорость влечения, с обратным зна­ком. Схема образования присоединённой массы m₂ показана на рис.4. Частицы воздушного потока, лежав­шие в начальный момент в плоскости вращения ветряка АА и расположенные вне влияния ветряка,

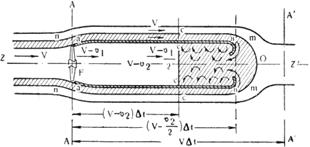
Рис. 4. Образование присоединённой массы.

за некоторый промежуток времени Dt передвинутся на расстояние V×Dt и займут положение А'А'. Частицы воздуха, лежащие в начальный момент внутри ометаемой площади и представ­ляющие начало струи, прошедшей через ветряк, за вре­мя Dt пройдут расстояние (V – v₂)×Dt и займут поло­жение СС. Вихревой же соленоид в эту минуту будет про­стираться от ветряка до сечения вв, имея длину .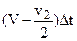

Таким образом, длина соленоида, образовавшегося за время Dt, будет на 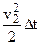больше длины колонны жидко­сти, прошедшей через ветряк. Часть соленоида cc–вв будет заполнена воздухом, засосанным соленоидом с конца вв. Эта масса воздуха и будет присоединённой массой.

Действительно, приращение количества движения мас­сы за время Dt мы можем выразить так: 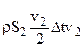. Отнеся к единице времени, получим: 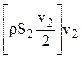, где выражение в квадратных скобках есть масса возду­ха, заключённая в отрезе соленоида ее–вв и v₂ – прира­щение скорости этой массы, или скорость влечения.

Слой жидкости с кольцеобразным сечением, заключён­ный между поверхностями ommccnn и аавв, заштрихо­ванный косыми линиями и образующий как бы стенки бутыли, идёт на образование присоединённой массы. В действительности явление происходит не так просто: соленоид при своём движении будет распадаться на от­дельные вихревые кольца, которые постепенно будут гаснуть, но количество движения, вызванное ими, будет сохраняться.

Напишем баланс энергии воздуха, протекающего через ветроколесо за одну секунду. Энергия, подводимая по­током, равна: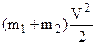

Энергия воспринятая ветряком: P(V – v₁).

Энергия, уносимая потоком в виде кинетической энергии: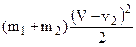

Потери, связанные с образованием присоединённой массы, подсчитанные по скорости влечения: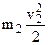

Уравнение баланса энергий получает следующий вид: 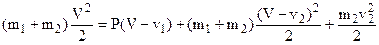(а)

Подставив в уравнение (а) значение P = (m₁+m₂)v₂и разделив на (m₁+m₂), получим:

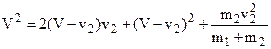(б)

Исключим из уравнения (б) m_l и m₂, подставив их зна­чения: m₁ = rS₂ (V – v₂) и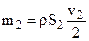

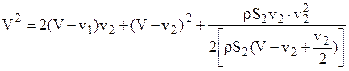
или: 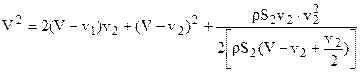(в)

Решая уравнение (в) относительно v₂ найдём: 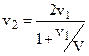(4) Это первая скоростная зависимость, отличающаяся от аналогичной в классической теории.

Напишем уравнение расхода, предполагая, что на ветряк, стоящий на одном месте, набегает поток со ско­ростью V (рис. 1): SV = S₁(V – v₁) = S₂(V – v₂),

откуда: 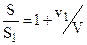и

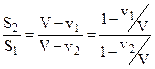
Подставляя сюда из уравнения (4) значение v ₂ /V, полу­чим: 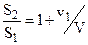(5)

Складывая выражения (а) и (б), получим: 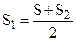(6) т. е. ометаемая площадь есть средняя арифметическая из площадей рабо­чей струи перед и позади ветряка.

Определение величины увлечённой массы (m₁ + m₂)даётся теоремой: увлечённая ветряком или решёткой мас­са жидкости не зависит от режима ветряка и проницаемо­сти решётки и равна объёму, описываемому в потоке ометаемой площадью, умноженному на плотность жидкости.

Воспользуемся уравнением (3), деля его обе части на v₂, и заменим m₁ и m₂ их значением:

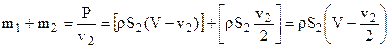
Подставляя сюда значение v₂ из уравнения (4) и S₂ из уравнения (5), получим:

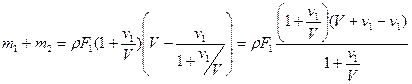
по сокращении получаем: m₁ + m₂ = rS₁V = Const. (7)

Лобовое давление на ветряк получаем из уравнения (3), подставив в него значение m₁+m₂ из уравнения (7): P = (m₁ + m₂)v₂ = rS₁Vv₂ (8)

Нагрузка на ометаемую площадь: 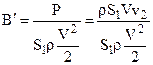(9) или: 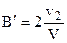. Подставляя сюда v₂ из уравнения (4), получаем: 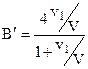, где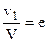

следовательно: 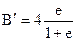(10) Принимая во внимание уравнение (9), получим лобо­вое давление Р равным: 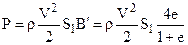(11)

Мощность на валу ветряка, согласно уравнению, равна: T = P(V – v₁). Подставив сюда значение Риз равенства (11),получим: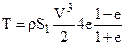

Коэффициент использования энергии ветра равен: 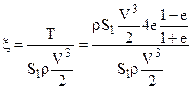(12)

по сокращении или (13)

Приравняв нулю первую производную выражения (12), получим:

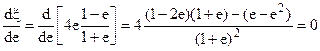
откуда: e = – 1 + 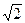= 0,414, т. е. максимум x получается,

когда 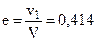, а не 0,333, как это было получено в классической теории.

Подставляя значение е в уравнение (12), получим: (14)

При этом нагрузка на сметаемую поверхность состав­ляет: 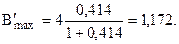(15)

В таблице 5 приведены для сравнения характерные величины идеального ветроколеса, полученные по классической теории П.Е. Жуковского и по теории Г.X. Сабинина.

Таблица 5

	Полная по­терянная скорость ветра за ветроколесом	Коэффициент нагрузки на ометаемую площадь В^1	Коэффициент тор­можения воздуш­ного по­тока v1/V при x mах	Наг­рузка В при x mах	Максималь­ный коэффициент исполь­зования энер­гии ветра x mах
Классиче­ская тео­рия	v2 = 2vl	4v 1 /V (1+v 1 /V)	0,333	0,888	0,593
Теория Г.X. Сабинина	v2= 2v1/(1+ v1/V)	4v1/V (1+v 1 /V)	0,414	1,172	0,687

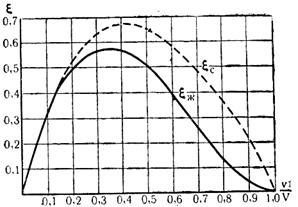
Для сравнения обеих теорий на рис. 5 показана зависимость x в функции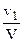

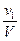Рис. 5. Изменение коэффициента использования энергии ветра x в зависимости от .

В заключение приведём основные положения класси­ческой теории и теории проф. Г.X. Сабинина.

1. По классической теории потеря скорости ветра за ветряком равна удвоенной потере скорости ветра в

плоскости ветряка, т.е. v₂ = 2v_l. По теории Г. X. Сабинина, это же уменьшение скорости ветра за ветряком выражается соотношением: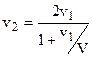

2. Осевое давление по классической теории: Р = m₁v₂, где m₁ = S_l (V – v₁). По теории проф. Сабинина, кроме массы воздуха, про­текающей через ометаемую поверхность ветроколеса, принимается во внимание масса воздуха m₂, засосанная внутрь вихревого соленоида из окружающего его потока.

Осевое давление равно: Р = (m₁ + m₂) v₂; при этом увлечённая ветряком масса

равна: m₁ + m₂ = rS₁V = сonst.

Практически нельзя построить ветряк с бесконечно большим числом лопастей, делающим бесконечно большое число оборотов и работающим без потерь, как это было сказано в определении идеального ветряка. В действитель­ности нам приходится иметь дело с реальным вет­ряком, который имеет конечное число лопастей (от 1 до 24), делает конечное число оборотов и работает с потерями.

Дата добавления: 2015-08-03